ray cylinder intersection formula-CodePudding

I am working on a simple raytracer, and I need to find a cylinder intersection, I found an equation that works for me. Still, I don't really understand its math demonstration, the formula is:

To hit a cylinder we notice that:

cylinder formula that I use

I use this website formula:

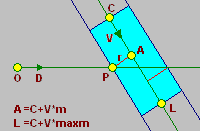
Definition:

C is the start cap point of the cylinder
V is a unit length vector that determines the cylinder's axis
r is the cylinder's radius
maxim determines the cylinder's end cap point

To hit a cylinder we notice that:

A = C   V*m
( P-A )|V = 0
   len( P-A ) = r

where m is a scalar that determines the closest point on the axis to the hit point. The P-A vector is perpendicular to V, which guarantees the closest distance to the axis. P-A is the cylinder's radius.

Solution:

(P-C-V*m)|V = 0

because p -c is perpendicular to V. we need to find m? (P-C)|V = m*(V|V) = m let (len(V)=1)

m = (D*t X)|V

expand result we reach:

m = D|V*t   X|V

let's solve the equation of the cylinder now:

len(P-C-V*m) = r

replace m and p-c with their values, we reach:

dot( D*t X - V*(D|V*t   X|V) ) = r^2

because the dot product of a vector with itself is the square of that vector. we factorize with (t) we get:

dot( (D-V*(D|V))*t   (X-V*(X|V)) ) = r^2

we have a general rule if we start with something like:

dot( A-V*(A|V) )

we end up with something like this:

A|A - (A|V)^2

And then we apply this rule to the line before, and we replace

dot( (D-V*(D|V))

with:

D|D - (D|V)^2

where we fill in D and X for A we move from:

dot( (D-V*(D|V))*t   (X-V*(X|V)) ) = r^2

to:

dot( (D|D - (D|V)^2)*t   (X|X - (X|V)^2) ) = r^2

so the formula can write as :

(A B)^2 = A^2   B^2   2AB

so our final formula is :

dot( (D|D - (D|V)^2)*t   (X|X - (X|V)^2) ) = (D|D - (D|V)^2)t^2   2 * t * (D-V*(D|V))|(X-V*(X|V))   (X|X - (X|V)^2)

so we reach :

(D|D - (D|V)^2)t^2   2 * t * (D-V*(D|V))|(X-V*(X|V))   (X|X - (X|V)^2) - r^2 = 0

so this formula is a quadratic formula in form of:

a*t^2   b*t   c = 0

that can be solved using:

so we can extract the three parameters a, b and c:

a = D|D - (D|V)^2

c = X|X - (X|V)^2 - r^2

b = 2 * (D-V*(D|V))|(X-V*(X|V)) =
 = 2 * (D|X - D|V*(X|V) - X|V*(D|V)   (D|V)*(X|V)) =
 = 2 * (D|X - (D|V)*(X|V))

I hope this explanation would help someone.