Polynomial approximation does not represent accurate approximation of line passing through data poin-CodePudding

I am working on the task where I have to Augment the data. For data augmentation, I have to do polynomial approximation of the data (Non linear data). But if I do the polynomial approximation, I am not getting an accurate approximation of the data.

Below are 35 points which I used as an original data.

x = [0.7375, 0.7405, 0.7445, 0.7488, 0.7515, 0.7545, 0.7593, 0.7625, 0.7657, 0.7687, 0.7715, 0.776, 0.7794, 0.7826, 0.7889, 0.7916, 0.7945, 0.8011, 0.8038, 0.8079, 0.8125, 0.8168, 0.8233, 0.826, 0.8287, 0.8318, 0.8361, 0.8391, 0.845, 0.8506, 0.8534, 0.8563, 0.8595, 0.8625, 0.8734]

y = [7797.61, 7829.59, 7833.6, 7837.02, 7854.76, 7862.18, 7893.06, 7927.04, 7946.49, 7975.83, 8038.12, 8110.94, 8115.37, 8125.11, 8172.58, 8182.54, 8215.06, 8232.01, 8274.98, 8272.71, 8243.45, 8242.93, 8225.08, 8199.25, 8180.92, 8143.29, 8152.09, 8136.59, 8164.3, 8202.04, 8203.57, 8174.67, 8192.0, 8201.25, 8131.32]

Below picture describes you more.

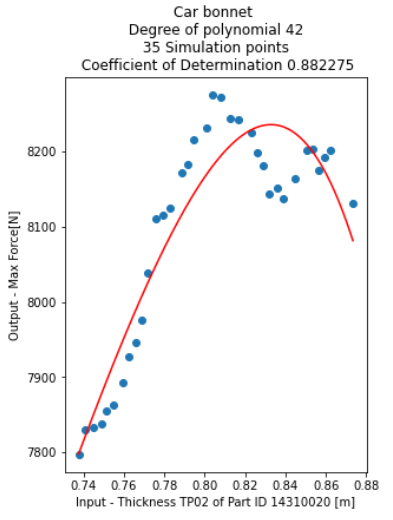
I have used from sklearn.preprocessing import PolynomialFeatures.

x_plot = np.linspace(min(x), max(x), 1000)

model = make_pipeline(PolynomialFeatures(42), Ridge(alpha=1e-3))
model.fit(x, y)
y_plot = model.predict(x_plot)
r2 = model.score(x,y)

Where x and y is my original data, 35 points.

I want to get closest to perfect (more accurate) approximation as obtained curve does not represent the accurate enough.

CodePudding user response：

You're doing something risky and I'm not sure you realize it. For N data points, an N degree polynomial can always fit the data exactly. Your plot is a degree 42 polynomial for 35 data points. You are certainly overfitting.

Perfect performance should never be the goal for fitting a model - the ability to generalize to unseen data should be the ultimate goal. Consider reading about overfitting online to better understand the problem here

CodePudding user response：

Your method is sensitive to the value of alpha in Ridge. The docs for scikit-learn say that you can use RidgeCV instead of Ridge to choose alpha based on leave-one-out cross validation, for example:

model = make_pipeline(
    PolynomialFeatures(...),
    RidgeCV(alphas=np.logspace(-10, 10)))

If you're just trying to approximate a curve passing through all those points, you could get a close curve with a SplineTransformer, without needing to use a high polynomial degree. For example:

model = make_pipeline(
    SplineTransformer(n_knots=5, degree=3),
    RidgeCV(alphas=np.logspace(-10, 10)))

The last two points on your graph concern me: you can find a polynomial or spline curve that comes close to both of them, but now you're assuming the shape of data between them, based on a very small amount of information. Overfitting, like @MikeL said. Any error in measurement of the last point would change your model much more than error in, say, the 5th point.