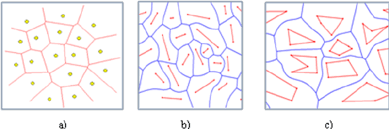
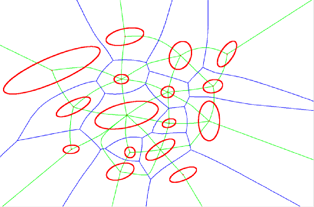
I've studied Voronoi Diagrams and Fortune's Algorithm before. What I'm curious about is if there's a generalization of Voronoi diagrams where instead of the input being a set of points, it is instead a set of non-intersecting curves in the plane, where we want to partition the plane into regions based off the Euclidean distance to the nearest curve.

Is this problem well defined and is there any known (hopefully efficient) algorithm to compute this generalization?

I've tried searching for an answer to this, but most resources seem to focus on curved metric spaces or curved regions rather than the input set itself being composed of non-points.

Edit: If this isn't well defined for non-intersecting curves, will it work for line segments?

CodePudding user response：

Yes, the Voronoi diagram is defined for arbitrary point sets and other distances than Euclidean. A quick web search gives you as many examples as you want. Intersecting curves are also possible.

The construction of the diagram for a set of line segments is well documented. The cells are bounded by line segments and parabolic arcs. If I am right, Fortune's algorithm generalizes to this case.

For general curves, the problem gets harder. In all cases, you need to derive the equation of bisector lines, and intersect them correctly to delimit the proper arcs at triple points.

A digitized version (on a raster grid) is easier and will work with any kind of shape. It is similar to the computation of a distance map, and can be performed in time linear in the number of pixels.