ggplot2 stat_density_2d: how to fix polygon errors at the dataset bounding box edges?-CodePudding

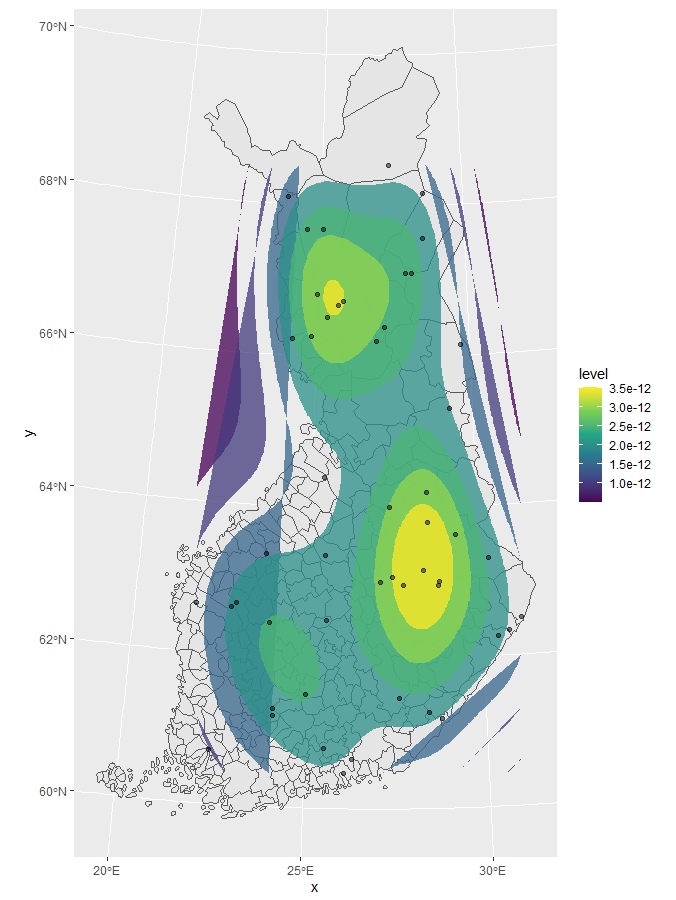
I am analysing my sfc_POINT dataset using ggplot2::stat_density_2d. I seems, though, that the resulting polygons get all wonky at the edge of the dataset bounding box. For whatever reason, ggplot2 can't seem to draw polygons further than the source dataframe edges.

How do I fix the density polygons? Is there a way to extend the bounding box for stat_density_2d somehow?

For this question I am able to reproduce my problem with a random sample point data. Please see the code here:

library(dplyr)
library(sf)
library(geofi)
library(ggplot2)

# Finland municipalities
muns <- geofi::get_municipalities(year = 2022)

# Create sample points
points <- sf::st_sample(muns, 50) %>% as.data.frame()
points[c("x", "y")] <- sf::st_coordinates(points$geometry)

p4 <- ggplot()  
  geom_sf(data = muns)  
  coord_sf(default_crs = sf::st_crs(3067))  
  stat_density_2d(geom = "polygon", 
                  data = points, 
                  aes(x = x, y = y, fill = ..level..), 
                  alpha = 0.75)  
  scale_fill_viridis_c()  
  geom_point(data = points, aes(x = x, y = y), alpha = 0.5)
p4

CodePudding user response：

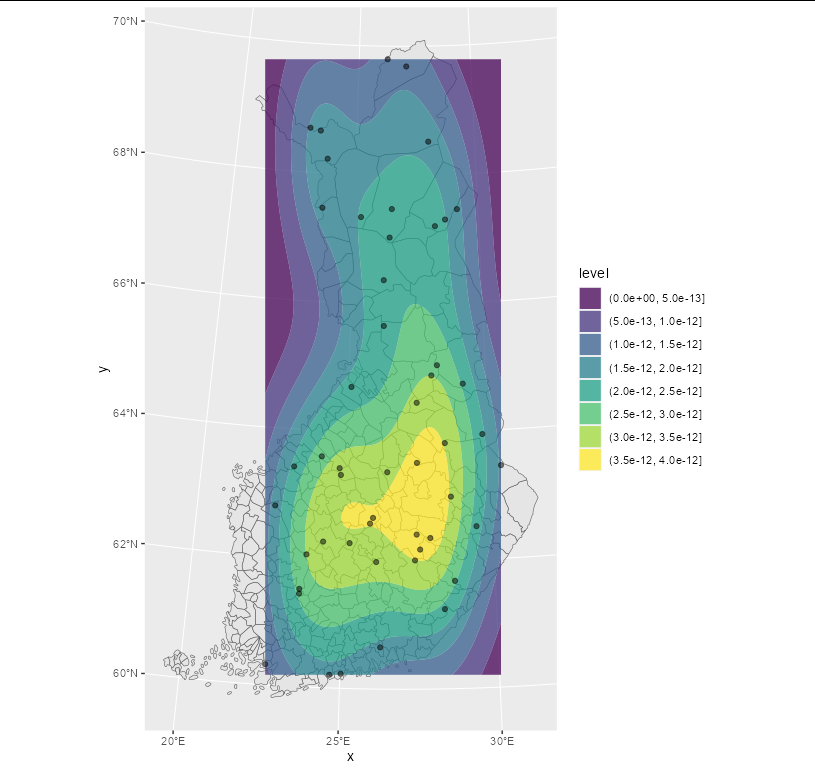
The "crazy polygons" phenomenon was an old problem that was often encountered when this method (calculating polygons via stat_density2d) was the only option. It was was remediated by the addition of geom_density2d_filled in ggplot2 v3.3.2

ggplot()  
  geom_sf(data = muns)  
  coord_sf(default_crs = sf::st_crs(3067))  
  geom_density2d_filled(
                  data = points, 
                  aes(x = x, y = y), 
                  alpha = 0.75)  
  geom_point(data = points, aes(x = x, y = y), alpha = 0.5)

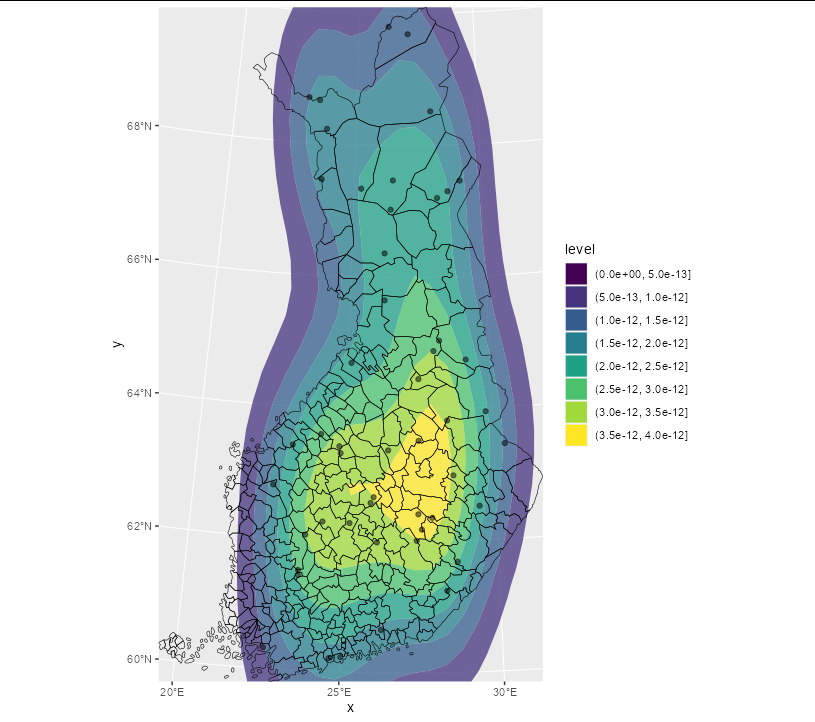
If you want to cover the whole range of muns rather than just the range of points, you can pre-calculate the density yourself over the bounding box of muns and pass that to geom_contour_filled:

d <- MASS::kde2d(points$x, points$y, lims = st_bbox(muns)[c(1, 3, 2, 4)])
dens <- data.frame(expand.grid(x = d$x, y = d$y), z = as.vector(d$z))

ggplot()  
  geom_contour_filled(data = dens, aes(x = x, y = y, z = z, 
                                       alpha = after_stat(level)))  
  geom_sf(data = muns, fill = NA, color = "black")  
  coord_sf(default_crs = sf::st_crs(3067), expand = FALSE)  
  geom_point(data = points, aes(x = x, y = y), alpha = 0.5)  
  scale_alpha_manual(values = c(0, rep(0.75, 7)), guide = "none")