lmer and lm - use all factor levels as 'control' group-CodePudding

In the case when there's a categorical variable (unordered factor) in a linear model or lmer formula the function uses the first factor level as the 'control' group for contrasts. In my case I have a categorical variable with several levels and would like for each level to be the 'control' base group. Is there a function that automates this process and creates a nice matrix with p-values for all combinations? Here's a sample code using the diamonds dataset.

library(lmer);library(lmerTest)    
#creating unordered factor
diamonds$color=factor(sample(c('red','white','blue','green','black'),nrow(diamonds),replace=T))
#lmer formula with factor in fixed effects
mod=lmer(data=diamonds,carat~color (1|clarity))
summary(mod,corr=F)

As show in the summary, 'black' is used as the control, so I would like all the other colors to be used as control.

Linear mixed model fit by REML. t-tests use Satterthwaite's method [ lmerModLmerTest] Formula: carat ~ color (1 | clarity) Data: diamonds

REML criterion at convergence: 64684

Scaled residuals: Min 1Q Median 3Q Max -2.228 -0.740 -0.224 0.540 8.471

Random effects: Groups Name Variance Std.Dev. clarity (Intercept) 0.0763 0.276 Residual 0.1939 0.440
Number of obs: 53940, groups: clarity, 8

Fixed effects: Estimate Std. Error df t value Pr(>|t|) (Intercept) 0.786709 0.097774 7.005805 8.05 0.000087 *** colorblue -0.000479 0.005989 53927.996020 -0.08 0.94 colorgreen 0.007455 0.005998 53927.990722 1.24 0.21 colorred 0.000746 0.005986 53927.988909 0.12 0.90 colorwhite 0.000449 0.005971 53927.993708 0.08 0.94
--- Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

CodePudding user response：

I could imagine wanting to do this for one of two reasons. First, would be to get the predicted value of the outcome at each level of the unordered factor (controlling for everything else in the model). The other would be to calculate all of the pairwise differences across the levels of the factor. If either of these is your goal, there are better ways to do it. Let's take the first one - generating predicted outcomes for each value of the factor holding everything else constant. Let's start by using the diamonds data and using the existing color variable, but making it an unordered factor.

library(lme4)
library(lmerTest)    
library(multcomp)
library(ggeffects)


  #creating unordered factor
data(diamonds, package="ggplot2")
diamonds$color <- as.factor(as.character(diamonds$color))

Now, we can run the model:

#lmer formula with factor in fixed effects
mod=lmer(data=diamonds,carat~color (1|clarity))

The function glht in the multcomp package tests pairwise differences among factor levels. Here is the output.



summary(glht(mod, linfct = mcp(color="Tukey")))
#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Multiple Comparisons of Means: Tukey Contrasts
#> 
#> 
#> Fit: lmer(formula = carat ~ color   (1 | clarity), data = diamonds)
#> 
#> Linear Hypotheses:
#>            Estimate Std. Error z value Pr(>|z|)    
#> E - D == 0 0.025497   0.006592   3.868  0.00216 ** 
#> F - D == 0 0.116241   0.006643  17.497  < 0.001 ***
#> G - D == 0 0.181010   0.006476  27.953  < 0.001 ***
#> H - D == 0 0.271558   0.006837  39.721  < 0.001 ***
#> I - D == 0 0.392373   0.007607  51.577  < 0.001 ***
#> J - D == 0 0.511159   0.009363  54.592  < 0.001 ***
#> F - E == 0 0.090744   0.005997  15.130  < 0.001 ***
#> G - E == 0 0.155513   0.005789  26.863  < 0.001 ***
#> H - E == 0 0.246061   0.006224  39.536  < 0.001 ***
#> I - E == 0 0.366876   0.007059  51.975  < 0.001 ***
#> J - E == 0 0.485662   0.008931  54.380  < 0.001 ***
#> G - F == 0 0.064768   0.005807  11.154  < 0.001 ***
#> H - F == 0 0.155317   0.006258  24.819  < 0.001 ***
#> I - F == 0 0.276132   0.007091  38.939  < 0.001 ***
#> J - F == 0 0.394918   0.008962  44.065  < 0.001 ***
#> H - G == 0 0.090548   0.006056  14.952  < 0.001 ***
#> I - G == 0 0.211363   0.006910  30.587  < 0.001 ***
#> J - G == 0 0.330150   0.008827  37.404  < 0.001 ***
#> I - H == 0 0.120815   0.007276  16.606  < 0.001 ***
#> J - H == 0 0.239602   0.009107  26.311  < 0.001 ***
#> J - I == 0 0.118787   0.009690  12.259  < 0.001 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> (Adjusted p values reported -- single-step method)

If you wanted all the predicted values of carat for the different values of color, you could us ggpredict() from the ggeffects package:

g <- ggpredict(mod, terms = "color")
plot(g)

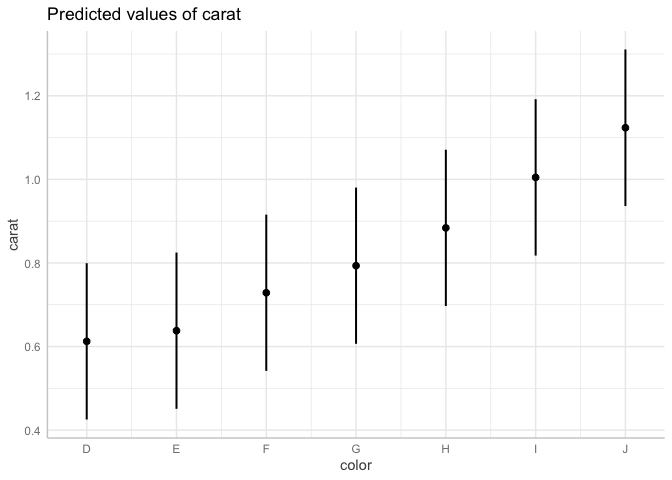
Plotting the g object produces the plot, but printing it will show the values and confidence intervals/

^{Created on 2023-02-01 by the reprex package (v2.0.1)}