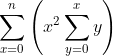I am trying to efficiently compute a summation of a summation in python:

Wolfram alpha is able to compute it too a high n value: sum of sum.

I have two approaches: a for loop method and an np.sum method. I thought the np.sum approach would be faster, however, they are the same until a large n, after which the np.sum has overflow errors and gives the wrong result.

I am trying to find the fastest way to compute this sum.

import numpy as np
import time

def summation(start,end,func):
    sum=0
    for i in range(start,end 1):
        sum =func(i)
    return sum

def x(y):
    return y

def x2(y):
    return y**2

def mysum(y):
    return x2(y)*summation(0, y, x)

n=100

# method #1
start=time.time()
summation(0,n,mysum)
print('Slow method:',time.time()-start)

# method #2    
start=time.time()
w=np.arange(0,n 1)
(w**2*np.cumsum(w)).sum()
print('Fast method:',time.time()-start)

CodePudding user response：

Here's a very fast way:

result = ((((12 * n   45) * n   50) * n   15) * n - 2) * n // 120

How I got there:

1. Rewrite the inner sum as the well-known x*(x 1)//2. So the whole thing becomes sum(x**2 * x*(x 1)//2 for x in range(n 1)).
2. Rewrite to sum(x**4 x**3 for x in range(n 1)) // 2.
3. Look up formulas for sum(x**4) and sum(x**3).
4. Simplify the resulting mess to (12*n**5 45*n**4 50*n**3 15*n**2 - 2*n) // 120.
5. Horner it.

CodePudding user response：

In fast numpy method you need to specify dtype=np.object so that numpy does not convert Python int to its own dtypes (np.int64 or others). It will now give you correct results (checked it up to N=100000).

# method #2
start=time.time()
w=np.arange(0, n 1, dtype=np.object)
result2 = (w**2*np.cumsum(w)).sum()
print('Fast method:', time.time()-start)

Your fast solution is significantly faster than the slow one. Yes, for large N's but already at N=100 it is like 8x times faster:

start=time.time()
for i in range(100):
    result1 = summation(0, n, mysum)
print('Slow method:', time.time()-start)

# method #2
start=time.time()
for i in range(100):
    w=np.arange(0, n 1, dtype=np.object)
    result2 = (w**2*np.cumsum(w)).sum()
print('Fast method:', time.time()-start)

Slow method: 0.06906533241271973
Fast method: 0.008007287979125977

CodePudding user response：

Does the formula change or do you want to efficiently calculate this particular sum?

For the latter you could just use the Gauss formula. See

Using this formula you can cut one loop. Making the algorithm a O(n) runtime instead of O(n^2)