Create a binary matrix after comparing columns' values in a dataframe-CodePudding

The text is long but the question is simple!

I have two dataframes that brings different informations about two variables and I need to create a binary matrix as my output after following some steps.

Let's say my dataframes are these:

market_values = pd.DataFrame({'variableA': (1,2.0,3), 'variableB': (np.nan,2,np.nan), 'variableC': (9,10,15), 'variableD' : (18,25,43),'variableE':(36,11,12),'variableF':(99,10,98), 'variableG': (42,19,27)})


   variableA  variableB  variableC  variableD  variableE  variableF  variableG
0        1.0        NaN          9         18         36         99         42
1        2.0        2.0         10         25         11         10         19
2        3.0        NaN         15         43         12         98         27


negociation_values = pd.DataFrame({'variableA': (0.1,0.2,0.3), 'variableB': (0.5,np.nan,0.303), 'variableC': (0.9,0.10,0.4), 'variableD' : (0.12,0.11,0.09),'variableE':(np.nan,0.13,0.21),'variableF':(0.14,np.nan,0.03), 'variableG': (1.4,0.134,0.111)})

   variableA  variableB  variableC  variableD  variableE  variableF  variableG
0        0.1      0.500        0.9       0.12        NaN        1.4      0.141
1        0.2        NaN        0.1       0.11       0.13        NaN      0.134
2        0.3      0.303        0.4       0.09       0.21       0.03      0.111

And I need to follow these steps:

1 - Check if two columns in my 'market_values' df have at least one 
    value that is equal (for the same row)
2 - If a pair of columns has one value that is equal (for the same row), 
    then I need to compare these same columns in my
    'negociation_values' df
3 - Then I have to discover which variable has the higher 
    negociation value (for a given row)
4 - Finally I need to create a binary matrix. 
    For those equal values' variable, I'll put 1 where one 
    negociation value is higher and 0 for the other. If a column 
    doesn't have an equal value with another column, I'll just put 1 
    for the entire column.

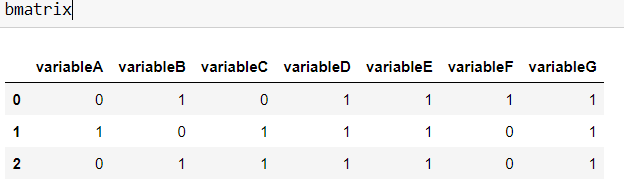
The desired output matrix will be like:

   variableA  variableB  variableC  variableD  variableE  variableF  variableG
0        0          1        0          1         1           1          1
1        1          0        1          1         1           0          1
2        0          1        1          1         1           0          1

The main difficult is at steps 3 and 4. I've done steps 1 and 2 so far. They're above:

arr = market_values.to_numpy()
is_equal = ((arr == arr[None].T).any(axis=1))
is_equal[np.tril_indices_from(is_equal)] = False
inds_of_same_cols = [*zip(*np.where(is_equal))]
equal_cols = [market_values.columns[list(inds)].tolist() for inds in inds_of_same_cols]

print(equal_cols)
-----------------

[['variableA', 'variableB'], ['variableC', 'variableF']]



h = []
for i in equal_cols:
    op = pd.DataFrame(negociation_values[i])
    h.append(op)

print(h)
-------

    [   variableA  variableB
 0        0.1      0.500
 1        0.2        NaN
 2        0.3      0.303,

    variableC  variableF
 0        0.9       0.14
 1        0.1        NaN
 2        0.4       0.03]

The code above returns me the negociation values for the columns that have at least one equal value in the market values df. Unfortunately, I don't know where to go from here. I need to write a code that says something like: "If variableA > variableB (for a row), insert '1' in a new matrix under variableA column and a '0' under variableB column for that row. keep doing that and then do that for the others". Also, I need to say "If a variable doesn't have an equal value in some other column, insert 1 for all values in this binary matrix"

CodePudding user response：

your negociation_values definition and presented table are not the same:

here is the definition I used

market_values = pd.DataFrame({'variableA': (1,2.0,3), 'variableB': (np.nan,2,np.nan), 'variableC': (9,10,15), 'variableD' : (18,25,43),'variableE':(36,11,12),'variableF':(99,10,98), 'variableG': (42,19,27)})
negociation_values = pd.DataFrame({'variableA': (0.1,0.2,0.3), 'variableB': (0.5,np.nan,0.303), 'variableC': (0.9,0.10,0.4), 'variableD' : (0.12,0.11,0.09),'variableE':(np.nan,0.13,0.21),'variableF':(1.4,np.nan,0.03), 'variableG': (0.141,0.134,0.111)})

The following code gives me the required matrix (though there are a number of edge cases you will need to consider)

cols = market_values.columns.values
bmatrix = pd.DataFrame(index=market_values.index, columns=cols, data=1)
for idx,col in enumerate(cols):
    print(cols[idx 1:])
    df_m = market_values[cols[idx 1:]]
    df_n = negociation_values[cols[idx 1:]]
    v = df_n.loc[:,df_m.sub(market_values[col],axis=0).eq(0).any()].sub(negociation_values[col], axis=0).applymap(lambda x: 1 if x > 0 else 0)
    if v.columns.size > 0:
        bmatrix[v.columns[0]] = v
        bmatrix[col] = 1 - v

The result is as required:

The pseudo code is:

for each column of the market matrix: subtract from the later columns, keep columns with any zeros (edge case: more than one column), from column with zero , find difference between corresponding negoc. matrix, set result to 1 if > 0, otherwise 0, enter into binary matrix

Hope that makes sense.