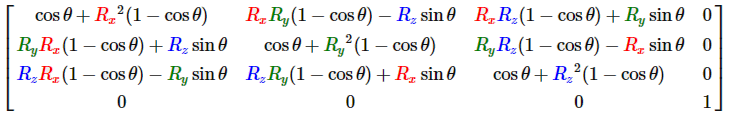Mapping coordinates from plane given by normal vector to XY plane (From 3D to 2D)-CodePudding

I have set of 3-dimensional dots, which lie on the plane with arbitrary normalized normal N' and the point through which this plane passes M (0, 0, 0) .

And to display it I need to map this coordinates to XY plane (convert from 3D to 2D).

First, what i do it's calculate dot product with N' and Z-axis as rotation angle Theta(N' ∙ Vec3f(0, 0, 1)) and multiply it by PI and divide by 180 (cos functions take radians).

Then i calculate cross product of N' and Z-axis (N' x Vec3f(0, 0, 1)) to get a new vector R (an arbitrary axis around which we will rotate our points).

Then i normalize R' = R / ||R||.

And pass it to next matrix:

But at the output, after matrix-vector multiplication, my points do not become two-dimensional(z is not 0), tell me please, what am I doing wrong?

CodePudding user response：

To get angle between N and Z, you have to calculate arccosine of dot product (assuming N is unit length)

Theta = acos(N.dot.Z)

and result is in radians.