How to draw tangential circles to the inside of a curve in Python using numpy and matplotlib in Pyth-CodePudding

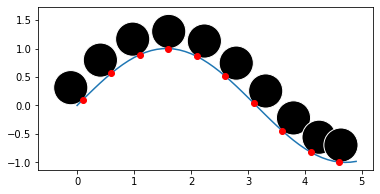
I would like to plot circles which are tangents to the interior of a curve in Python as shown below:

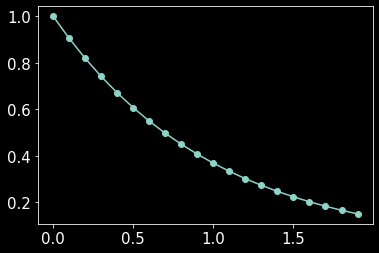
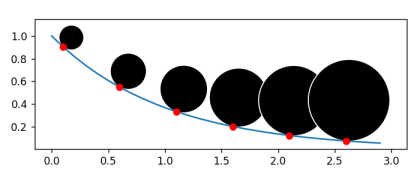
I tried the following approach. I created an inverted exponential curve to get the curve as shown below.

x = np.arange(0, 2, 0.1)
y = [1/np.exp(i) for i in x]
plt.plot(x, y, marker = "o")

To add a circle as tangent to the curve, I am adding a circle manually as follows:

fig, ax = plt.subplots()

#Plot exponential curve
ax.plot(x, y)

#Add tangential circle manually
pi = np.pi
c1 = plt.Circle((x[1]  np.sin(pi/4) * 0.1, y[1]   np.sin(pi/4) * 0.1),
                radius = 0.1, facecolor = "black", ec = "white")
ax.add_patch(c1)

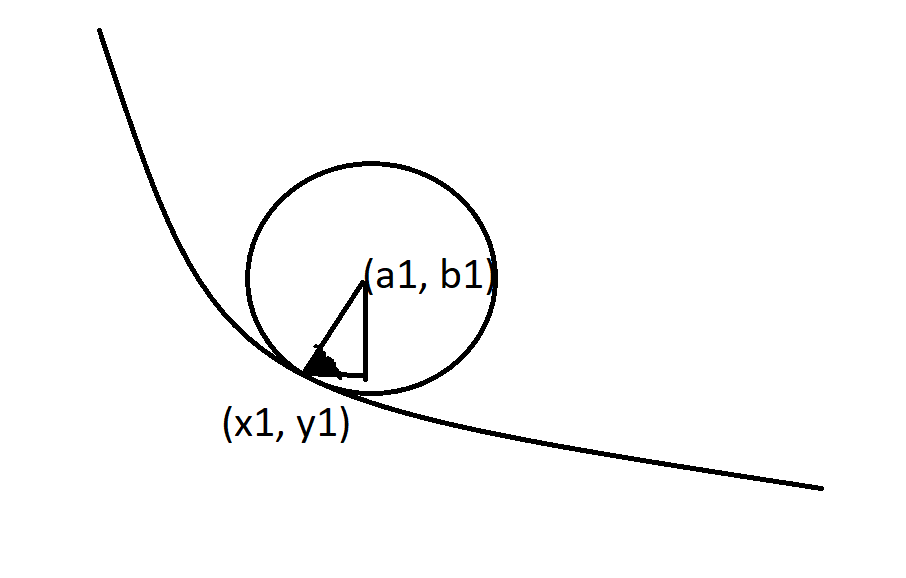
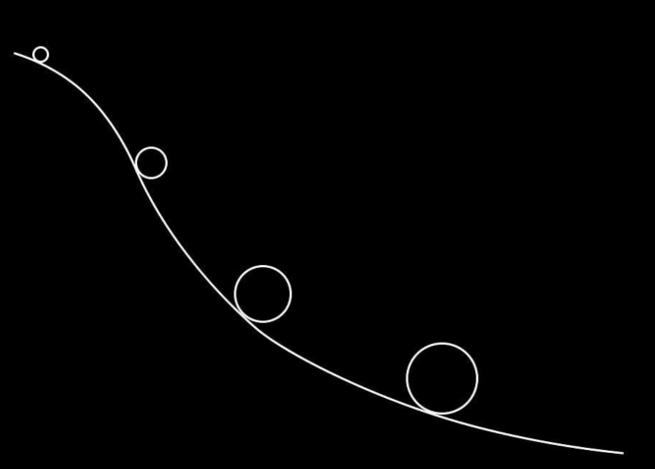
Here my assumption is that the angle denoted by the shaded part in the figure below (between the normal radius and horizontal x-axis is 45 degrees).

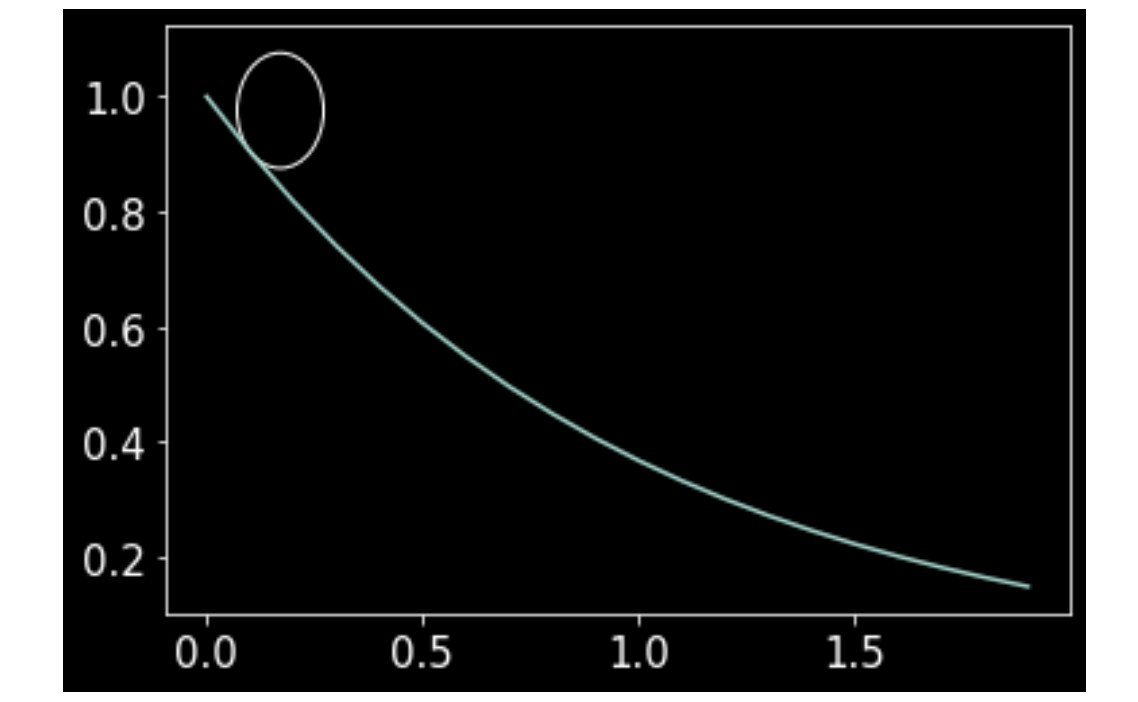
However, I think this is an incorrect assumption and incorrect way to do it. When I add more circles, they are not exactly tangential to the curve as shown below.

What would be the correct approach to draw the circles as tangents to the curve? Is it possible to do it in Python?

CodePudding user response：

Using trigonometry (there is likely a way to simplify but I'm rusty tired :p).

fig, ax = plt.subplots()

X = np.arange(0, 5, 0.1)
Y = np.sin(X)

#Plot exponential curve
ax.plot(X, Y)
ax.set_aspect('equal')

#Add tangential circles
for i in np.arange(1,len(X),5):
    ax.plot(X[i], Y[i], marker='o', color='r')
    pi = np.pi
    radius = 0.3
    # slope of tangent
    dydx = np.gradient(Y)[i]/np.gradient(X)[i]
    # slope of perpendicular
    slope = 1/abs(dydx)
    # angle to horizontal
    angle = np.arctan(slope)
    c1 = plt.Circle((X[i] - np.sign(dydx)*np.cos(angle) * radius,
                     Y[i]   np.sin(angle) * radius),
                    radius = radius, facecolor = "black", ec = "white")
    ax.add_patch(c1)

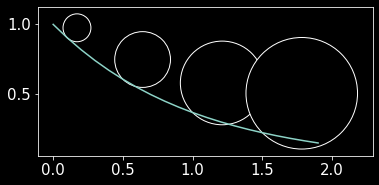
output:

CodePudding user response：

Your function is exp(-x)

It's derivative is -exp(-x), so tangent vector at point x, exp(-x) is (1, -exp(-x)) and normal vector is (exp(-x), 1) (note sign change).

Normalize it

n_len = np.hypot((y)[i], 1)
nx = y[i] / n_len
ny = 1 / n_len

center for radius R is

c1 = plt.Circle((x[i]   R * nx, y[i]   R * ny, ...

CodePudding user response：

For the circle to be tangent, its center must be located along the normal to the curve (this is a straight-line with slope -δx/δy).

You did not specify how the radius varies, so there are two options:

the radius is a function of x or y or s (curvilinear abscissa) that you supply; then place the center at the desired distance from the contact point, on the normal;
the radius is such that it matches the local curvature; then what you want is the osculating circle; there is a formula to compute the radius of curvature.

https://en.wikipedia.org/wiki/Osculating_circle