Given the following labelled data:

feature_matrix = np.array \
    (
        [
            [   1,    1],
            [   2,    3],
            [   3,    4],
            [-0.5, -0.5],
            [  -1,   -2],
            [  -2,   -3],
            [  -3,   -4],
            [  -4,   -3]
        ]
    )

labels = np.array \
    (
        [
             1,
             1,
             1,
            -1,
            -1,
            -1,
            -1,
            -1
        ]
    )

The idea is to run the linear perceptron algorithm through the labelled data until convergence in order to find the resulting parameter θ and offset parameter θ₀. For reference, here is the perceptron function I wrote in python:

def perceptron(feature_matrix, labels, convergence=True):

    # initialize theta and theta_0 to zero
    theta = np.zeros(len(feature_matrix[0])); theta_0 = 0

    while convergence:
        for i in range(len(feature_matrix)):

            exit = True

            if (labels[i] * np.dot(feature_matrix[i], theta) <= 0):

                theta   = theta     labels[i] * feature_matrix[i]
                theta_0 = theta_0   labels[i]

                exit = False

        if exit: break

    return (theta, theta_0)

I have used this code before, and can confirm that it works. The exit flag makes sure that the loop breaks if there are no mistakes, however, the resulting parameters apparently are not correct. So, the perceptron algorithm is initialised with the parameters to zero, i.e θ=[0,0] and θ₀=0. The first datapoint to be explored is (1,1). Below are the values the function returns after it converges:

parameters = perceptron(feature_matrix, labels)

print('Theta_0:', parameters[-1])
print('Theta  :', parameters[0].tolist())

# Theta_0: 1
# Theta  : [1.0, 1.0]

These values seem off, since the decision boundary sits right on top of the datapoint (-0.5,-0.5) as can be seen in a desmos graph 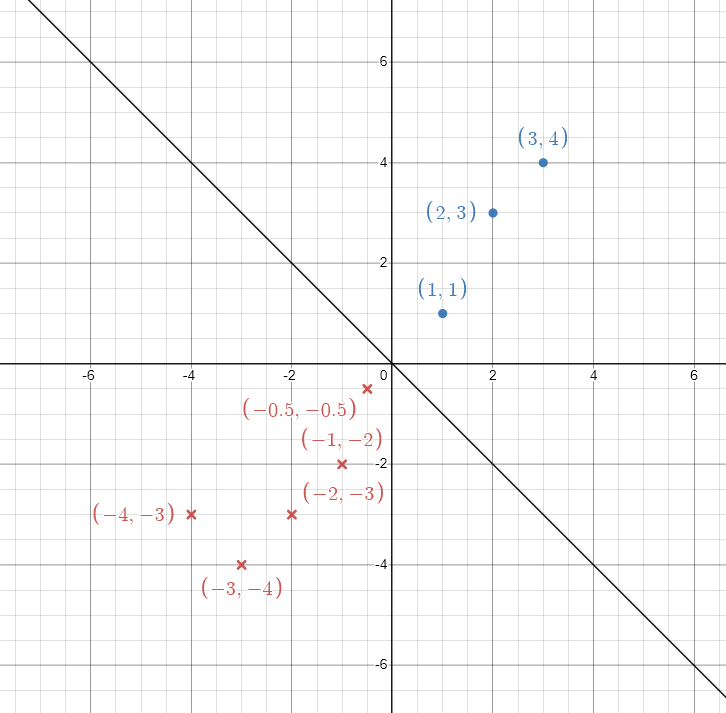In general there are infinitely many solutions that perceptron might end up in.

Note, that the classical perceptron algorithm converges (not just numerically, but actually stops and succeeds with 100% accuracy) with no learning rates, etc. as long as your data is linearly separable, and this dataset clearly is.

So the final code will look something like this:

def perceptron(feature_matrix, labels, convergence=True):

    # initialize theta and theta_0 to zero
    theta = np.zeros(len(feature_matrix[0]));
    theta_0 = 0

    while convergence:
        # FIRST FIX, initialisation outside the loop
        exit = True
        for i in range(len(feature_matrix)):
            # SECOND FIX, theta_0 used in error criterion
            if (labels[i] * (np.dot(feature_matrix[i], theta)   theta_0) <= 0):
                theta   = theta     labels[i] * feature_matrix[i]
                theta_0 = theta_0   labels[i]

                exit = False

        if exit: break

    return (theta, theta_0)

CodePudding user response：

"I have used this code before, and can confirm that it works".

Your code is never supposed to work. Here's why - the entire theory of perceptron algorithm is based on four things:

1. forward pass of the data through the perceptron
2. activation function
3. error computation
4. backpropagation of error

Your code only has the first one, but the last three are missing. Those three components are arguably the most important parts of a perceptron network. You also need to have a learning rate, since just backpropagating the entire error will never lead to convergence of the network.

The following code is based on