Finding a hierarchy of polygons-CodePudding

I need an algorithm to determine a hierarchy of polygons. For example,

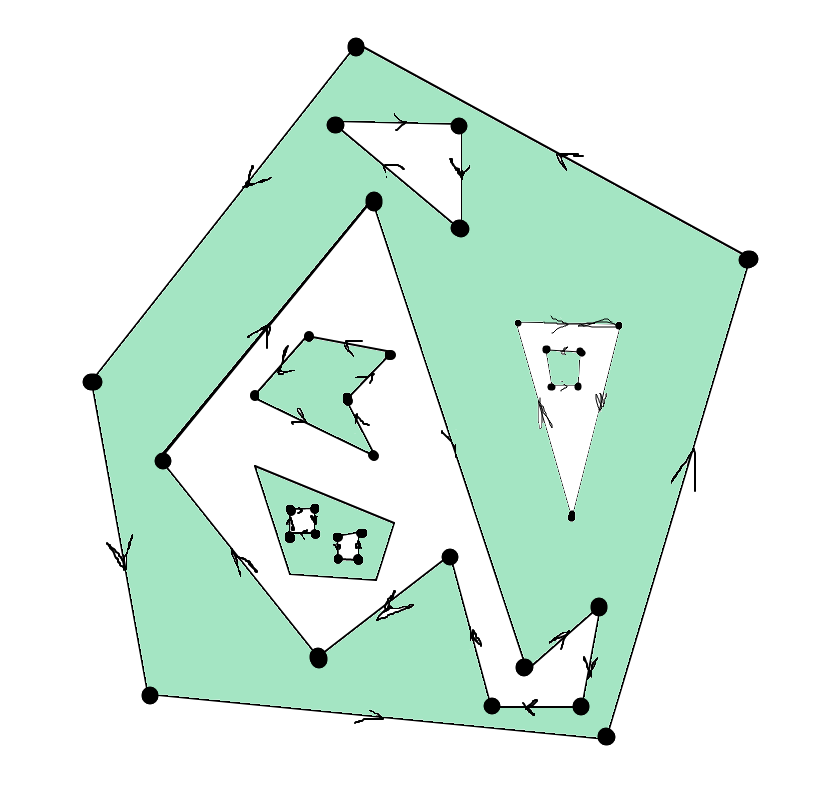
I have only closed loops of vertices, where polygons have CCW vertices order and holes have CW vertices order. I want to create a structure to contain such hierarchy of polygons and holes.

using Loop = std::vector<Point>;

class PolygonHierarchy
{
public:
    PolygonHierarchy(const std::vector<Loop>& loops);
    ~PolygonHierarchy();

private:
    class Polygon
    {
    public:
        std::vector<Point> vertices;
        std::vector<Polygon*> childPolygons;
        bool isCCWOrder;
    }

    std::vector<Polygon*> polygonHierarchies;
}

Can someone explain how to find child polygons and form such tree? (it's not necessary to provide code).

CodePudding user response：

As per what @YvesDaoust said in the comments, for each polygon/hole, you can find all the polygons/holes which contain it.

This will give you a directed graph. In this graph, for each node, you may have more than one incoming edges. For instance, something like this:

1 (a)
|\
| \
|  2 (b)
3 /

Here, both 1 and 2 know about 3, but ideally only 2 should. Here, 1 is a parent of 2. If you generalise this, since there wont be any intersecting polygons, if you have two conflicting nodes a and b, and if a is an ancestor of b, you can discard a (otherwise discard b), and you can continue in this fashion, until only one incoming edge remains for each node,