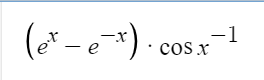I've got a bunch of functions that I can use, and they are used many times per second. I would like to know how to evaluate which functions affect my calculation times the most.

How could I go about it?

I'm trying to find out specifically how demanding is:

compared to other commonly used functions such as SquareRoot(X), cube of (x), sigmoid etc?

CodePudding user response：

Typically, most mathematical functions like that would be evaluated in constant time. This simply means that there is a finite number of instructions used, regardless of the value of the input parameter. Often by a single instruction, but sometimes by a short loop.

The computational complexity says nothing about the actual time to evaluate the function, only how it would grow with the input parameter. So if you want to measure the actual performance you need to do actual measurements.

Usually when discussion computational complexity it is assumed that the values fit in whatever data-type is used, i.e. you would not need to handle arbitrary precision math.

As a rule of thumb, simple instructions, like addition or multiplication are single digit number of instructions, things like division in the lower double digits, and some 'complex' instructions like trigonometry can go up to three digits. 'slow' in this context would still be measured in nanoseconds, so still very fast unless you need to compute it millions of times.