Translate quaternion rotation to correct frame-CodePudding

I place an IMU on my wrist and extend my arm as shown in the photo below. I spin in a circle once, while my arm remains in the fixed position. I calculate the

Question:

What changes should I make to measure the angle from the quaternion? ( I suspect it is in form of

Which is coherent with the assumption that w is the first coordinate of your quaternion, and that you indeed rotate mostly around z.

Euler angles (Or more likely Tait Bryan angles) are a different way to represent a rotation. A rotation is represented by a composition of 3 elemental rotations. These 3 rotations are sometimes called yaw, pitch and roll. If you want to fully represent your rotation, you will have to calculate all of these 3 elemental rotations:

table = readtable("sample_data.csv", 'Delimiter', ',');

w = table.w;
x = table.x;
y = table.y;
z = table.z;

[yaw,pitch,roll] = getAngles(w, x, y, z);

quaternion_angles = getQuaternionAngle(w);

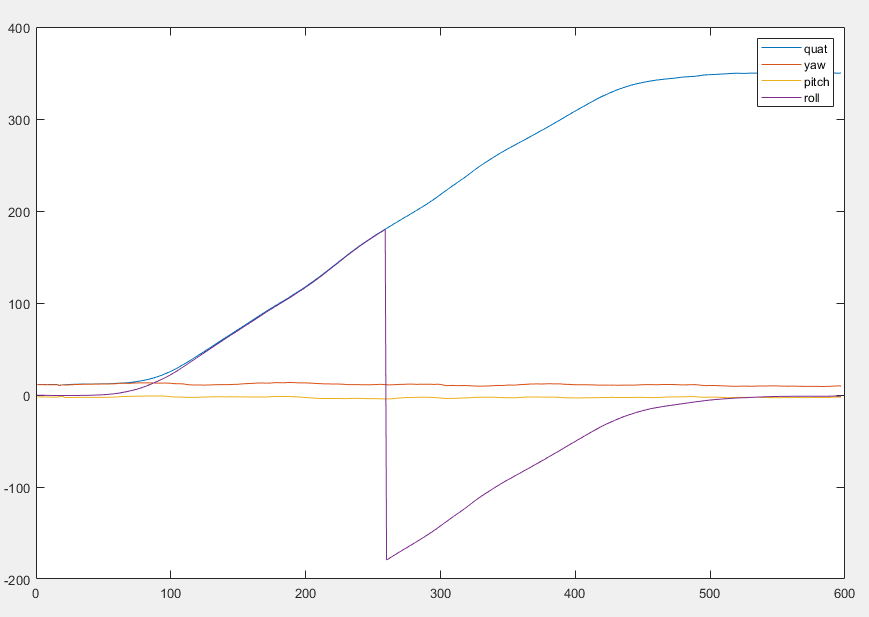
figure; plot([quaternion_angles,yaw,pitch,roll]);

legend({'quat','yaw','pitch','roll'})

function angle = getQuaternionAngle(w)

    angle = 2*acosd(w);
    
end

function [yaw,pitch,roll] = getAngles(w, x, y, z)
    
    yaw = atan2d(2*(y.*z   w.*x), w.*w - x.*x - y.*y   z.*z);
    pitch = asind(-2*(x.*z-w.*y));
    roll = atan2d(2*(x.*y   w.*z), w.*w   x.*x - y.*y - z.*z);

end

See? The angle around Z is represented by the roll (the discontinuity is due to the use of arctan). When you rotate around yourself, the angle increases steadily between 0 and 360º. You can also see that you have a bit of yaw, i.e your IMU is a bit tilted