Is there a way to vectorize calculating interest dollars dependent on previous dollar values-CodePudding

I am doing a simulation of yearly cash flows and having interest applied to each year's cumulative balance. My current algorithm is done by looping through each row to calculate the interest and add the interest to the end balance for next year's starting balance. The issue is that I need to have this run for many simulation years many times, and the run time becomes increasingly longer. Is there a way vectorize this algorithm or to implement other workarounds to reduce run time? Thanks!

This example is done with an interest rate of 5%

I've looked into using the lag() function to calculate the cumulative balance and interest each simulation year, but this would require using lag() a number of times equal to the number of simulated years in order to calculate the end balance and runs into the same issue of run time.

A SAS implementation uses the RETAIN statement in the DATA step. The algorithm runs quickly in SAS but I'm looking for an R implementation.

CodePudding user response：

I don't think there's a way to avoid using a loop here (or hiding a loop in Reduce as I've done), as you are dependent on the previous row to calculate the current row.

But you should be able to do this with relative speed as once you have the end_balance you can figure out the rest without having to loop:

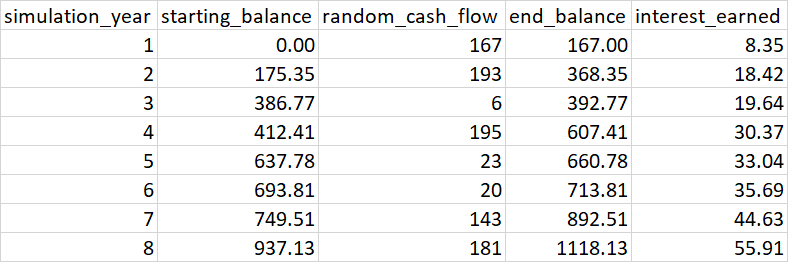
simflow <- function(cash_flow, rate) {
    end_balance <- Reduce(\(x,y) x*(1   rate)   y, cash_flow, accumulate=TRUE)
    data.frame(
        starting_balance = end_balance - cash_flow,
        cash_flow,
        end_balance,
        interest_earned = end_balance * rate
    )
}

cash_flow <- c(167,193,6,195,23,20,143,181)
simflow(cash_flow, rate=0.05)
##  starting_balance cash_flow end_balance interest_earned
##1           0.0000       167    167.0000         8.35000
##2         175.3500       193    368.3500        18.41750
##3         386.7675         6    392.7675        19.63838
##4         412.4059       195    607.4059        30.37029
##5         637.7762        23    660.7762        33.03881
##6         693.8150        20    713.8150        35.69075
##7         749.5057       143    892.5057        44.62529
##8         937.1310       181   1118.1310        55.90655

100 years replicated 100,000 times in ~ 35 seconds:

system.time({
    replicate(100000, simflow(sample(cash_flow, 100, replace=TRUE), rate=0.05))
})
##   user  system elapsed 
##  35.19    0.36   35.55

CodePudding user response：

A first step might be to think about this problem as calculating simultaneously many simulations, e.g., 100000, and then increment each year. So after 100 years the balance is

set.seed(123)
n_rep = 100000; n_year = 100
starting_balance <- rep(0, n_rep)
for (i in 1:n_year) {
    random_cash_flow <- runif(n_rep, 100, 200)
    end_balance <- starting_balance   random_cash_flow
    interest_earned <- end_balance * 0.05
    ## starting balance 'after' year i
    starting_balance <- end_balance   interest_earned
}

and a summary is

> summary(starting_balance)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 362182  402658  411041  411045  419490  462818

the computation takes a fraction of a second.