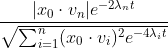How should I change the different size `n=100,200,300,400` so that the `h1t` function of these value-CodePudding

Following this question:

#make this example reproducible
set.seed(100001)
n <- 500
#Sample GOE random matrix
A <- matrix(rnorm(n*n, mean=0, sd=1), n, n) 
G <- (A   t(A))/sqrt(2*n)
ev <- eigen(G)
l <- ev$values
v <- ev$vectors

#size of multivariate distribution
mean <- rep(0, n) 
var <- diag(n)
#simulate bivariate normal distribution
initial <- MASS::mvrnorm(n=1, mu=mean, Sigma=var) #ten random vectors
#normalized the first possible initial value, the initial data uniformly distributed on the sphere
x_0 <- initial/norm(initial, type="2")

# improved function
h1t <- function(t) {
  h10 <- c(x_0 %*% v[, n])
  denom <- vapply(t, function(.t) {
    sum((x_0 %*% v)^2 * exp(-4*(l - l[n]) * .t))
  }, numeric(1L))
  abs(h10) / sqrt(denom)
}

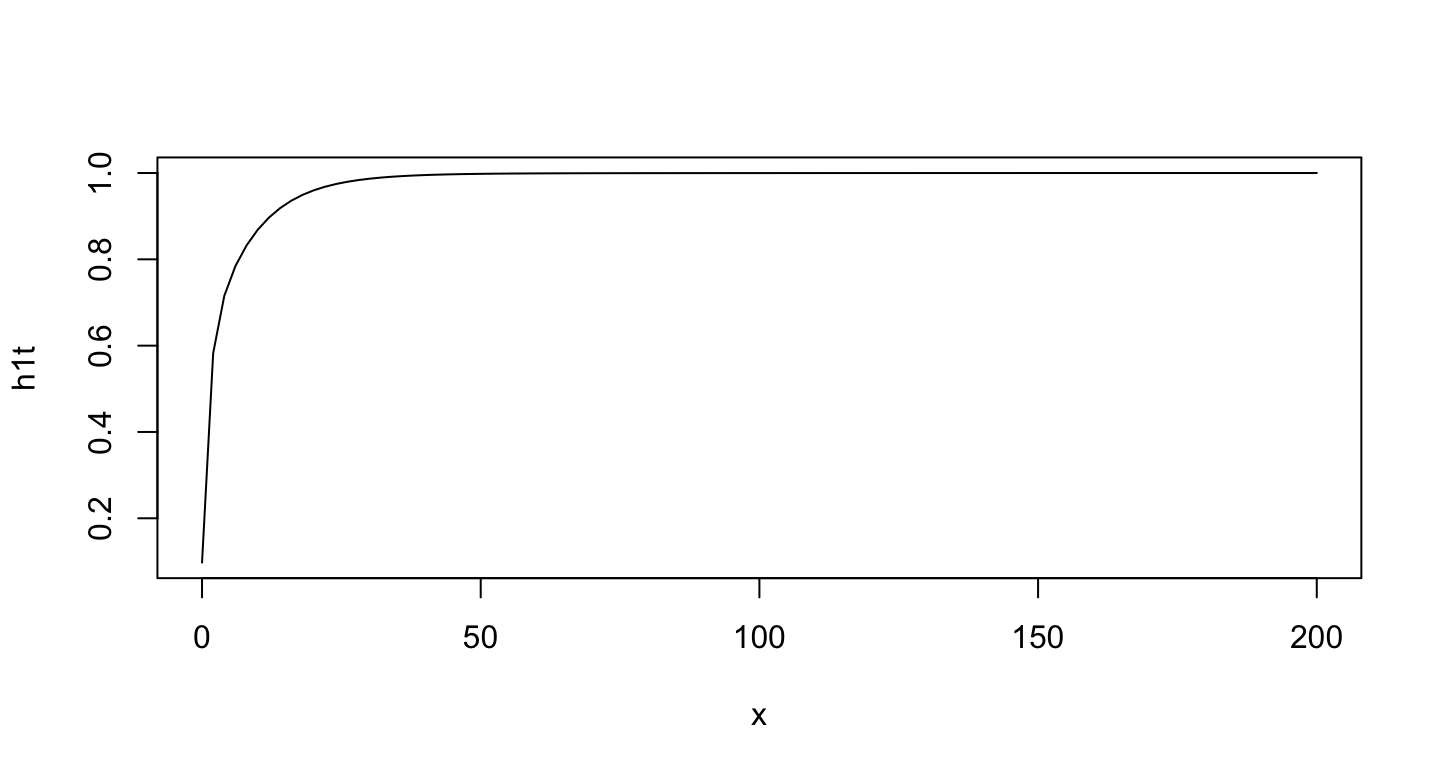
plot(h1t, from = 0, to = 200)

The plot for n=500:

I repeat the above code for n=100

#make this example reproducible
set.seed(100001)
n <- 100
#Sample GOE random matrix
A <- matrix(rnorm(n*n, mean=0, sd=1), n, n) 
G <- (A   t(A))/sqrt(2*n)
ev <- eigen(G)
l <- ev$values
v <- ev$vectors

#size of multivariate distribution
mean <- rep(0, n) 
var <- diag(n)
#simulate bivariate normal distribution
initial <- MASS::mvrnorm(n=1, mu=mean, Sigma=var) #ten random vectors
#normalized the first possible initial value, the initial data uniformly distributed on the sphere
x_0 <- initial/norm(initial, type="2")

# improved function
h1t <- function(t) {
  h10 <- c(x_0 %*% v[, n])
  denom <- vapply(t, function(.t) {
    sum((x_0 %*% v)^2 * exp(-4*(l - l[n]) * .t))
  }, numeric(1L))
  abs(h10) / sqrt(denom)
}

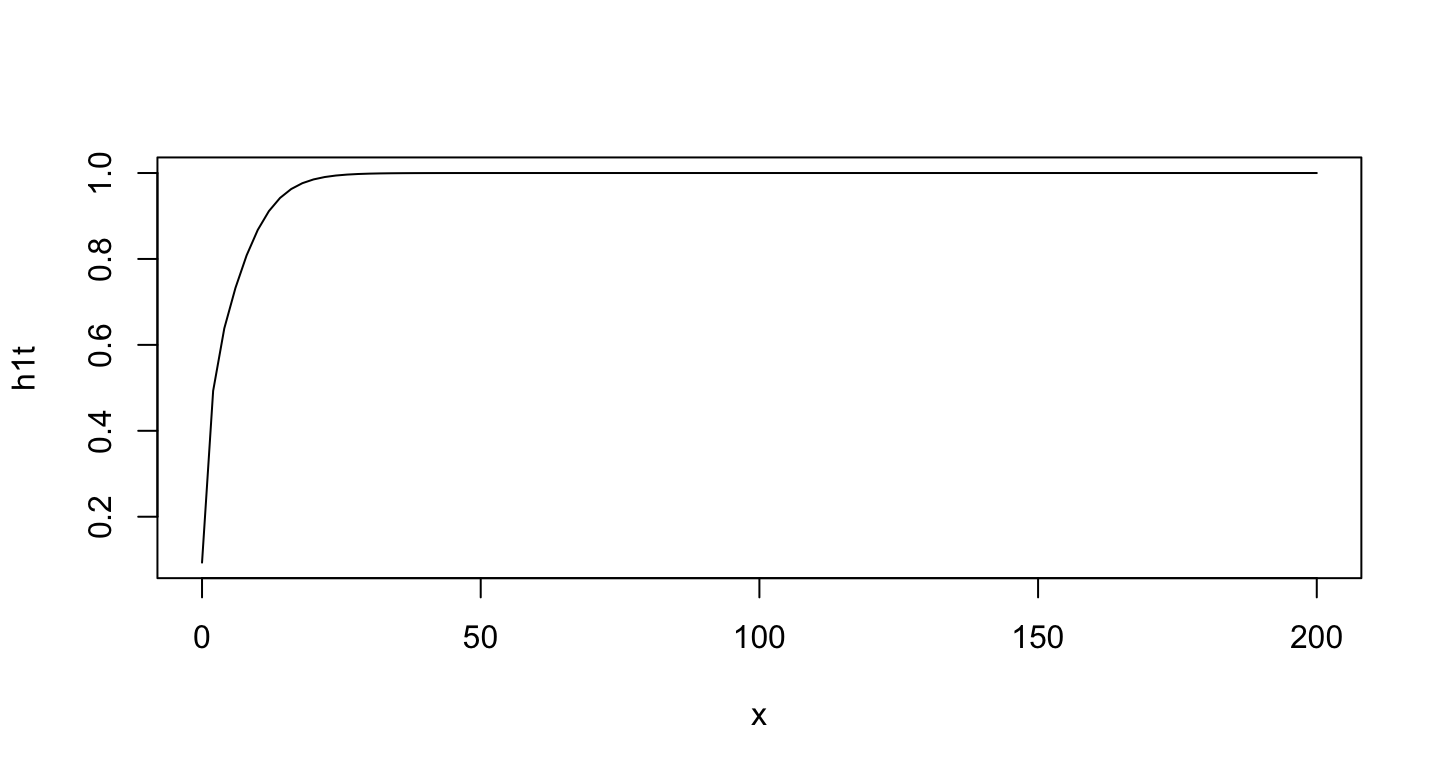
plot(h1t, from = 0, to = 200)

The plot for n=100:

Question: How should I change the different size n=100,200,300,400 so that the h1t function of these values n are in the same plot?

CodePudding user response：

You can do this by wrapping everything in the function, then using a for loop (or lapply) to plot the individual lines:

h1t <- function(t, n = 500) {
  set.seed(100001)
  A <- matrix(rnorm(n*n, mean=0, sd=1), n, n) 
  G <- (A   t(A))/sqrt(2*n)
  ev <- eigen(G)
  l <- ev$values
  v <- ev$vectors
  
  mean <- rep(0, n) 
  var <- diag(n)
  initial <- MASS::mvrnorm(n=1, mu=mean, Sigma=var) #ten random vectors
  x_0 <- initial/norm(initial, type="2")
  
  h10 <- c(x_0 %*% v[, n])
  denom <- vapply(t, function(.t) {
    sum((x_0 %*% v)^2 * exp(-4*(l - l[n]) * .t))
  }, numeric(1L))
  abs(h10) / sqrt(denom)
}

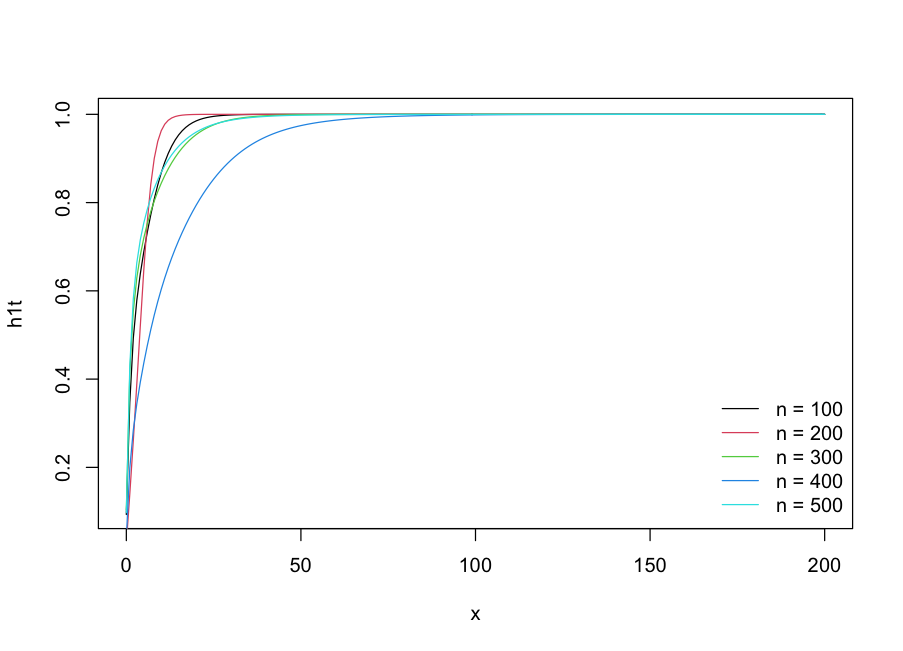
Create a blank plot and draw the lines:

plot(h1t, n = 500, from = 0, to = 200, type = "n") 
for(xx in seq(100, 500, 100)){
  lines(x = seq(0, 200, 1), y = h1t(t = seq(0, 200, 1), n = xx), col = xx/100)
}
legend("bottomright", paste0("n = ",(seq(100, 500, 100))), 
       lty = 1, col = 1:5, bty = "n")

### or lapply
# plot(h1t(t = seq(0, 200, 1), n = 500), type = "n")
# lapply(seq(100, 500, 100), function(x) lines(x = seq(0, 200, 1), 
#                                             y = h1t(t = seq(0, 200, 1), n = x), 
#                                             col = x/100))
# legend("bottomright", paste0("n = ",(seq(100, 500, 100))), 
#       lty = 1, col = 1:5, bty = "n")

Result: