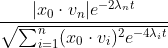How to get the value of `t` so that my function `h(t)=epsilon` for a fixed `epsilon`?-CodePudding

Following this question:

If I have generated m=1000 random vectors x_0 uniformly distributed on the sphere and eigenvectors of a random matrix GOE:

#make this example reproducible
set.seed(101)
n <- 500
#Sample GOE random matrix
A <- matrix(rnorm(n*n, mean=0, sd=1), n, n) 
G <- (A   t(A))/sqrt(2*n)
ev <- eigen(G)
l <- ev$values
v <- ev$vectors

#sample 1000 x_0
#size of multivariate distribution
mean <- rep(0, n) 
var <- diag(n)

#simulate bivariate normal distribution
initial <- MASS::mvrnorm(n=1000, mu=mean, Sigma=var) #ten random vectors
#normalized the first possible initial value, the initial data uniformly distributed on the sphere
xmats <- lapply(1:1000, function(i) initial[i, ]/norm(initial[i, ], type="2"))

Define a function h_1(t):

The code for this function is that

# function
h1t <- function(t,x_0) {
  h10 <- c(x_0 %*% v[, n])
  denom <- vapply(t, function(.t) {
    sum((x_0 %*% v)^2 * exp(-4*(l - l[n]) * .t))
  }, numeric(1L))
  abs(h10) / sqrt(denom)
}

I want to find t_epsilon so that h(t_epsilon)=epsilon for epsilon=0.01.

EDIT:

Following the answer:

find_t <- function(x, epsilon = 0.01, range = c(-50, 50)) {
  uniroot(function(t) h1t(t, x) - epsilon, range,
          tol = .Machine$double.eps)$root
}

res <- lapply(xmats, find_t)

However, it shows that error

Error in uniroot(function(t) h1t(t, x) - epsilon, range, tol = .Machine$double.eps) : 
f() values at end points not of opposite sign

CodePudding user response：

uniroot finds where your function is equal to 0, so you need a wrapper function that subtracts epsilon from your function's output:

find_t <- function(x, epsilon = 0.01, range = c(-50, 50)) {
  uniroot(function(t) h1t_modefied(t, x) - epsilon, range,
          tol = .Machine$double.eps)$root
}

We could use this one at a time on your different matrices to find the t value where the output is equal to epsilon:

x_01t <- find_t(x_01)
x_01t
#> [1] -0.5149889

h1t_modefied(x_01t, x_01)
#> [1] 0.01

Or, better still, put all your matrices in a list and run the function on all of them with a simple single call to lapply:

xmats <- list(x_01 = x_01, x_02 = x_02, x_03 = x_03, x_04 = x_04, x_05 = x_05)

res <- lapply(xmats, find_t)

res
#> $x_01
#> [1] -0.5149889
#> 
#> $x_02
#> [1] -0.2521749
#> 
#> $x_03
#> [1] -0.02756945
#> 
#> $x_04
#> [1] -0.4903002
#> 
#> $x_05
#> [1] -0.3473344

And we can see that these are the t values that make your hit_modefied function output epsilon by feeding these results back into the function via Map:

Map(h1t_modefied, t = res, x_0 = xmats)
#> $x_01
#> [1] 0.01
#> 
#> $x_02
#> [1] 0.01
#> 
#> $x_03
#> [1] 0.01
#> 
#> $x_04
#> [1] 0.01
#> 
#> $x_05
#> [1] 0.01