Find xy coordinates of a point knowing its distance to other 2 points-CodePudding

I'm writing a code in R to calculate the xy coordinates of point, using the law of cosines. I have two reference points (1 and 2) which the xy coordinates are known. I want to find the coordinates of the other point (3). I know the distances 3-1, 3-2 and 1-2, but I don't know the angles between them.

Thanks in advance for any help!

I've tried some trigonometric equations I've found on web and Rohlf&Archie 1978 paper, but they don't work.

CodePudding user response：

You haven't told us your set-up exactly, but it sounds as though you have two known x, y, co-ordinates:

x1 <- 1
x2 <- 5

y1 <- 3
y2 <- 6

And known distances between these two points plus a third point:

d12 <- 5
d13 <- 8
d23 <- 5

We can draw them like this:

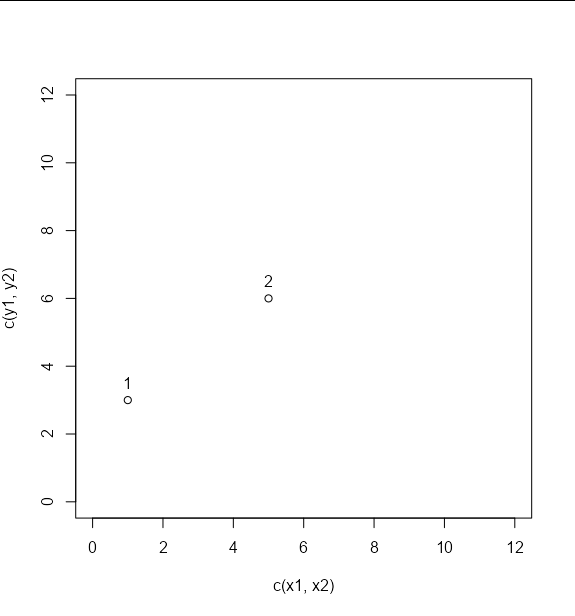
plot(c(x1, x2), c(y1, y2), xlim = c(0, 12), ylim = c(0, 12))
text(c(x1, x2), c(y1, y2)   0.5, labels = c('1', '2'))

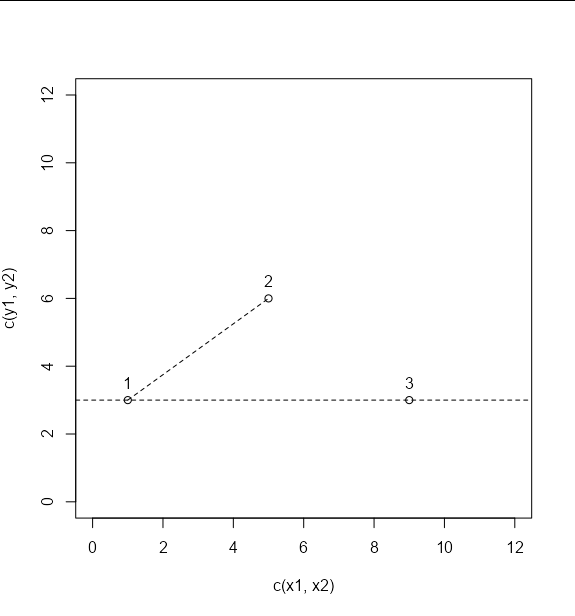
Now, it's obviously easy to calculate the angle between the horizontal line and the segment joining points 1 and two - it's just the arctangent of the slope:

abline(h = y1, lty = 2)
theta <- atan2(y2 - y1, x2 - x1)

segments(x1, y1, x1   d12 * cos(theta), y1   d12 * sin(theta), lty = 2)

Now, although we don't know where point 3 is, we can use the law of cosines to calculate the angle 3-1-2 like this:

angle_312 <- acos((d12^2   d13^2 - d23^2)/(2 * d12 * d13))

To get this in terms of angle from the horizontal we can do:

angle_13 <- angle_312 - theta

This allows us to work out the co-ordinates of point 3:

x3 <- x1   d13 * cos(angle_13)
y3 <- y1   d13 * sin(angle_13)

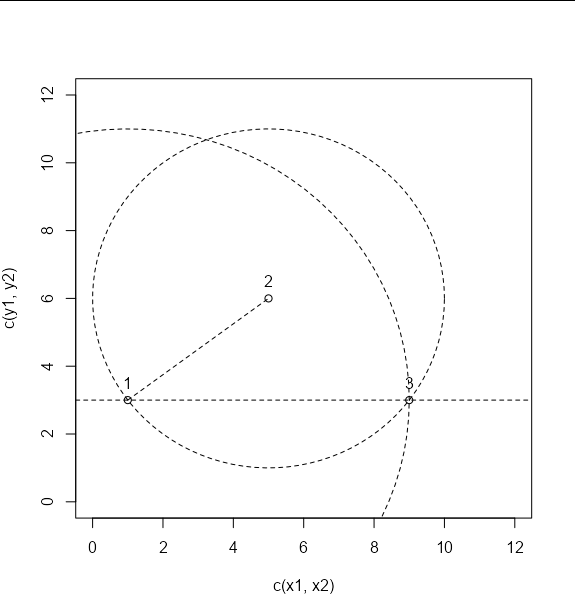
We can draw this point on our plot as follows:

points(x3, y3)
text(x3, y3   0.5, '3')

And we can show that it is correct by drawing circles of the correct radius around points one and two. Point 3 should be at the meeting point of the two circles:

polygon(x1   dist_1_3 * cos(seq(0, 2 * pi, length = 100)), 
        y1   dist_1_3 * sin(seq(0, 2 * pi, length = 100)), lty = 2)
polygon(x2   dist_2_3 * cos(seq(0, 2 * pi, length = 100)), 
        y2   dist_2_3 * sin(seq(0, 2 * pi, length = 100)), lty = 2)

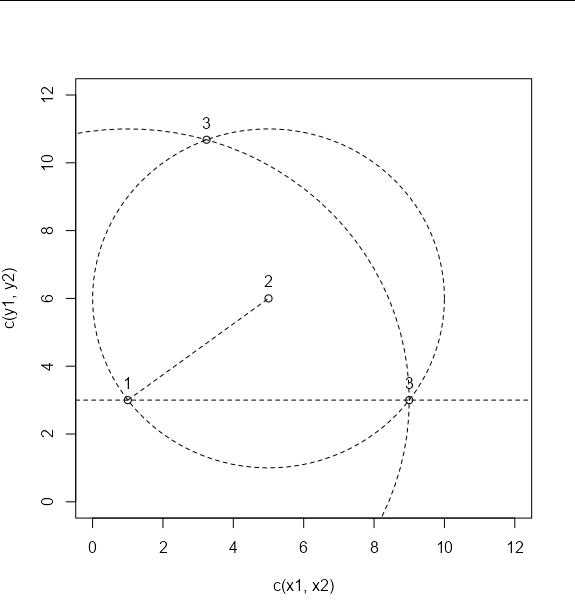
Note that there is a second solution at the other point where the circles meet: in this case we would get that by changing angle_13 <- angle_312 - theta to angle_13 <- angle_312 theta:

angle_13 <- angle_312   theta

x3 <- x1   d13 * cos(angle_13)
y3 <- y1   d13 * sin(angle_13)

points(x3, y3)
text(x3, y3   0.5, '3')

CodePudding user response：

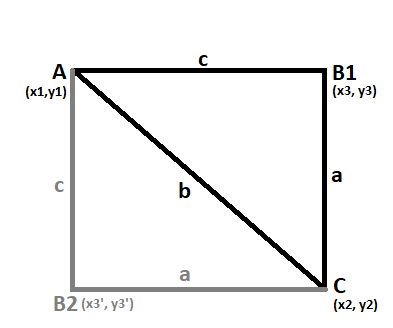
Suppose we are using the following conditions:

pointA <- c(x1 = 1, y1 = 1)
pointC <- c(x2 = 4, y2 = 1)

AC <- sqrt(
  (pointA[["x1"]] - pointC[["x2"]])^2  
  (pointA[["y1"]] - pointC[["y2"]])^2
)

AB <- 4

BC <- 5

We are looking for coordinates of point B (points B1 and B2) (x3 and y3 / x3' and y3').

First we find cos and sin of angle C (ACB1 == ACB2 as CB1==CB2==a; AB1==AB2==c and AC=b is common):

cosC <-(AC^2   BC^2 - AB^2) / (2*AC*BC)
sinC <- sqrt(1-cosC^2)

It is obvious that there are two possible solutions for the conditions. Then the points will be

pointB1 <- c(x3 = pointC[["x2"]]   BC*cosC,
             y3 = pointC[["y2"]]   BC*sinC)

pointB2 <- c(x3 = pointC[["x2"]] - BC*cosC,
             y3 = pointC[["y2"]] - BC*sinC)

Now we can check the results:

> sqrt(
    (pointB1[["x3"]] - pointC[["x2"]])^2  
      (pointB1[["y3"]] - pointC[["y2"]])^2
  )
[1] 5
> sqrt(
    (pointB2[["x3"]] - pointC[["x2"]])^2  
      (pointB2[["y3"]] - pointC[["y2"]])^2
  )
[1] 5

The advantage of this solution that we do not call low precision acosfunction as well as other trigonometric functions. And use cosC / sinC as temporary variables only.