How to discretize a nonlinear system-CodePudding

How can i discretize the following nonlinear system. Im using Matlab and Casadi for Model Predictive Control. The Constant C is betwenn 0 and 1.

dx/dt = C * x/(x^2   1)

Thank you for your time and Help.

CodePudding user response：

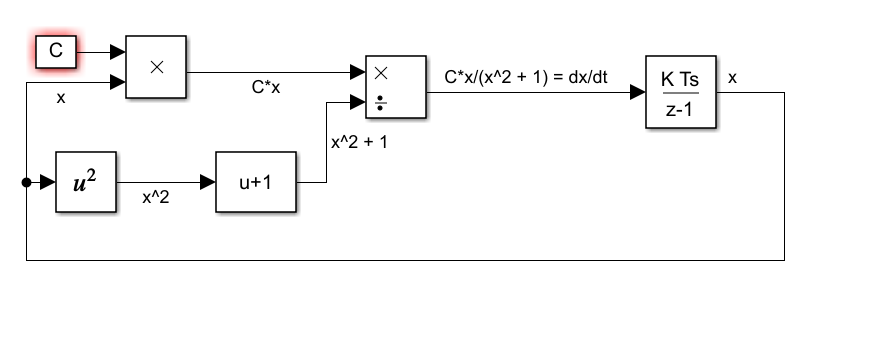
If you are just looking to build it from blocks, something like this should work:

You basically need to invert the formula to:

x = int(C * x/(x^2   1))

Everything to the right of the equal sign then feeds the input to the integrator and the output of the integrator becomes x.

CodePudding user response：

Well if you want to use mfile to discretize a differential equation, there are a lot of methods such as simple Euler, Runge-Kutta, and so on. Let me say how to use Euler method. based on the differential definition:

dx/dt = (x(i 1) - x(i))/dt

here i is the discretization index and dt is sample time (typically 0.01). If I have to use your equation:

(x(i 1) - x(i))/dt = C*x(i)/(x(i)^2 1)

after simplification:

x(i 1) = x(i) dt*(C*x(i)/(x(i)^2 1))

this is your discretized model. In matlab, just use the following code:

C = 0.5;
N = 100;
x(1) = 1;       % initial condition
dt = 0.01;

i = 1;
for i = 1:N
    x(i 1) = x(i)   dt*(C*x(i)/(x(i)^2   1));
end