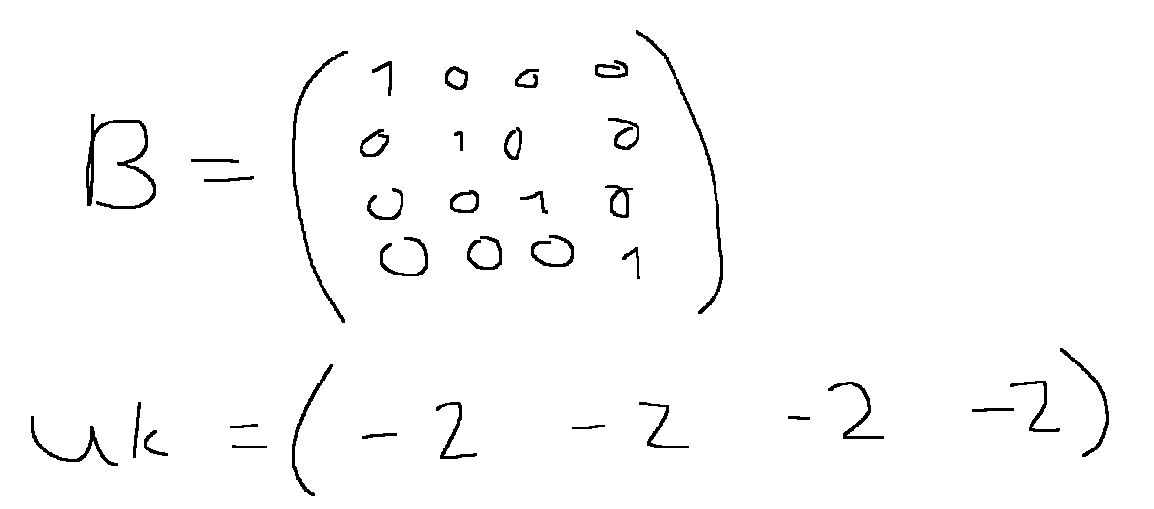Use the controlMatrix in the Kalman Filter Class | OpenCV,Python,NumPy-CodePudding

I am using OpenCV to track the position of a Contour.

After recieving the Position(x,y) i pass them to the kalman Filter.

Here an Example:

import cv2
import numpy as np

dt = 1
kalman = cv2.KalmanFilter(4,2,4)
kalman.measurementMatrix = np.array([[1,0,0,0],[0,1,0,0]],np.float32)
kalman.transitionMatrix = np.array([[1,0,dt,0],[0,1,0,dt],[0,0,1,0],[0,0,0,1]],np.float32)
kalman.controlMatrix = np.array([[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]],np.float32)


#RECIEVE X,Y Position from Contour 

mp = np.array([[np.float32(Contour_X)],[np.float32(Contour_Y)]])
kalman.correct(mp)
tp = kalman.predict()
PredictionX,PredictionY= int(tp[0]),int(tp[1])

So I defined a 4 dimensional transition matrix, a 2 Dimensional measurement matrix and a 4 dimensional control vector.

My Goal:

I am trying to slow down the value of my prediction with my control vector (like adding a friction), but i dont know how and the documentary shows no example. I really tried to understand it with the Docs :

One Idea i had was defining u_k-1 like that but i still dont know how to really implement it.

Anyone else faced this issue?

Thank you for reading

CodePudding user response：

Kalman Filter is a feedback control where the control, $u_k$ is implicitly calculated in the algorithm, as opposed to the open-loop control problem where the $u_k$ is more explicit. The control is, roughly speaking, calculated from how far your measurement is to the estimate, and how accurate your estimate really is.

Therefore, in addition to the transition and control matrix, you will need to define the covariance of the process noise, $\mat{Q}_k$. See code below for an example:

dt = 0.1
kalman = cv2.KalmanFilter(4,2,4)
kalman.measurementMatrix = np.array([[1,0,0,0],[0,2,0,0]],np.float32)
kalman.transitionMatrix = np.array([[1,0,dt,0],[0,1,0,dt],[0,0,1,0],[0,0,0,1]],np.float32)
kalman.controlMatrix = np.array([[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]],np.float32)
kalman.errorCovPre = np.array([[3.1, 2.0, 0., 0.],
                            [2.0, 1.1, 0., 0.],
                            [0., 0., 1.0, 0.],
                            [0., 0., 0., 1.0]], dtype=np.float32)


#RECIEVE X,Y Position from Contour 
Contour_X = 2
Contour_Y = 6

mp = np.array([[np.float32(Contour_X)],[np.float32(Contour_Y)]])
kalman.correct(mp)
tp = kalman.predict()
PredictionX,PredictionY= int(tp[0]),int(tp[1])

Play around with the covariance matrix to see how it affects the prediction. It is also interesting to look at the posteriori covariance, kalman.errorCovPost, and compare it with the priori covariance matrix.