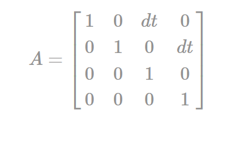I am using the KalmanFilter Class in OpenCV to predict a Point.

I am tracking an Contour that means i recieve an x,y Point of it.

So my Code looks like that:

First I say that I got 4 dynamic parameters and 2 measurement parameters. The way i understood it is that my tracked (x,y) Positions are my measurements and with the velocity of them i got 4 dynamic parameters

 #Give Input to Kalman class
kalman = cv2.KalmanFilter(4,2)
kalman.measurementMatrix = np.array([[1,0,0,0],[0,1,0,0]],np.float32)
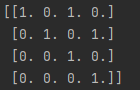
kalman.transitionMatrix = np.array([[1,0,1,0],[0,1,0,1],[0,0,1,0],[0,0,0,1]],np.float32)

After this i track my contour in opencv and pass the position to the class.

mp = np.array([[np.float32(center_x)],[np.float32(center_y)]])
kalman.correct(mp)
tp = kalman.predict()
PredictedPointx,PredictedPointy = int(tp[0]),int(tp[1])

And as a result i get 2 Predicted Points and my code works.

The thing is i dont know what exactly happens in this whole process.

I got some questions like

1. Why does my transition matrix look like this

And not like this :

2. Is it correct that i recieve the velocity after giving my 2 points?

3. Where are all the other Kalman values and calculations. For example the Kalman Gain and so on.

Can someone explain what exactly happens after passing in my x and y position.

Thank you for reading

CodePudding user response：

This post is too long for a comment, so I'll just parse it as an answer.

1.) What FPS are you working on and where did you find the transition matrix? If it is 1 FPS, then dt = 1 and your transition matrix is OK. If it is not 1 FPS, your velocity estimate will not be correct (or more precisely, it will not be what you'd expect). I believe the filter would still work properly, but output a velocity not measured in meters per second (or pixels per second), but instead based on meters per 1/FPS. I'm not entirely sure about that, so please leave a comment if you believe I am distributing nonsense ;-) Be aware that, as soon as you pass a process noise parameter, this starts to make a difference and you should set your dt properly.

2.) You should receive an estimate on the velocity as soon as you supply more than one point. Assuming the velocity does not change abruptly, the quality of the velocity estimate will improve with the number of points you feed to the filter.

3.) The Kalman gain is not a parameter of the Kalman filter. Given the assumptions of the filter, the optimal kalman gain is calculated during the iteration of the filter and used in the actual filtering (see K_t on the Kalman Filter Wikipedia page). The process noise and measurement noise covariance matrices are missing, but you can set them with processNoiseCov and measurementNoiseCov respectively (according to the documentation)