I'm trying to create a random float generator (range of 0.0-1.0), where I can supply a single target value, and a strength value that increases or decreases the chance that this target will be hit. For example, if my target is 0.7, and I have a high strength value, I would expect the function to return mostly values around 0.7.

Put another way, I want a function that, when run a lot of times, would produce a distribution graph something like this:

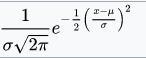and use 0.7 as mu to shift the distribution towards 0.7. I added a leading coefficient of 0.623 to shift the values to be between 0 and 1 and migrated it from formula to C#, this can be found below.

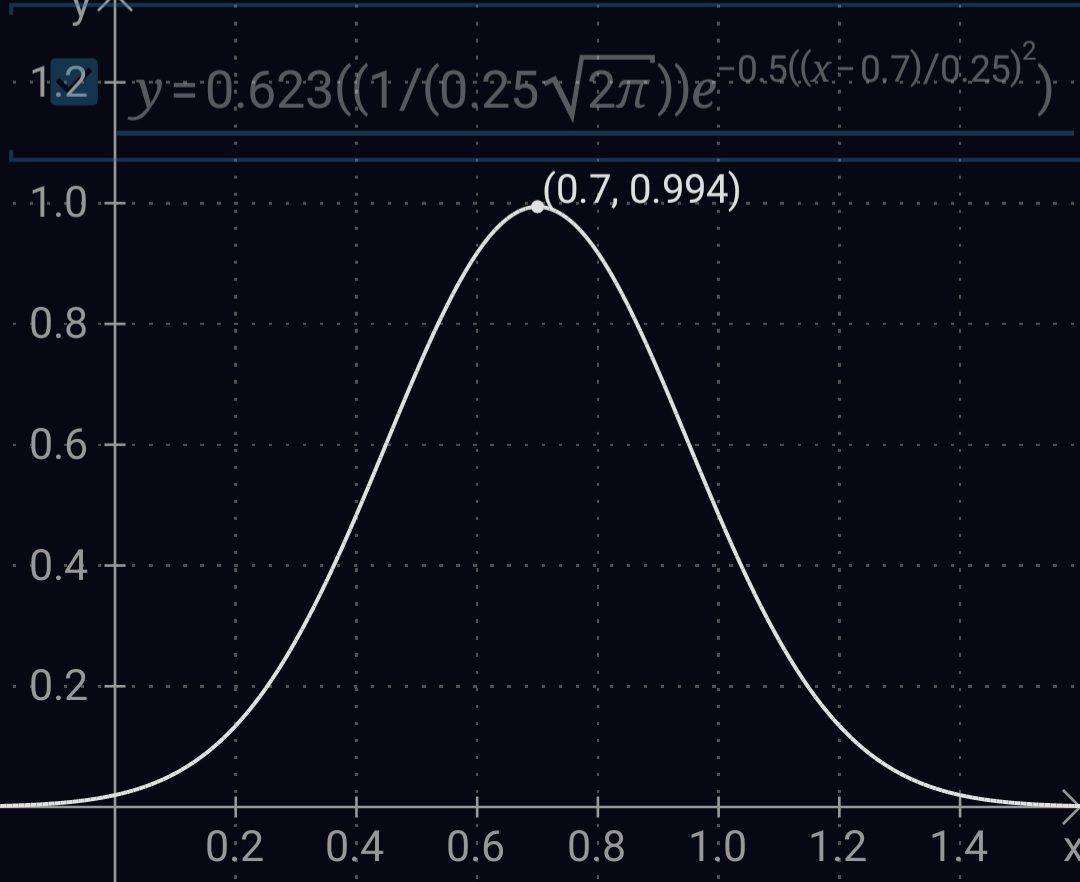
Usage:

DistributedRandom random = new DistributedRandom();

// roll for the chance to hit
double roll = random.NextDouble();

// add a strength modifier to lower or strengthen the roll based on level or something
double actualRoll = 0.7d * roll;

Definition

public class DistributedRandom : Random
{
    public double Mean { get; set; } = 0.7d;

    private const double limit = 0.623d;
    private const double alpha = 0.25d;
    private readonly double sqrtOf2Pi;
    private readonly double leadingCoefficient;

    public DistributedRandom()
    {
        sqrtOf2Pi = Math.Sqrt(2 * Math.PI);
        leadingCoefficient = 1d / (alpha * sqrtOf2Pi);
        leadingCoefficient *= limit;
    }

    public override double NextDouble()
    {
        double x = base.NextDouble();

        double exponent = -0.5d * Math.Pow((x - Mean) / alpha, 2d);

        double result = leadingCoefficient * Math.Pow(Math.E,exponent);

        return result;
    }
}

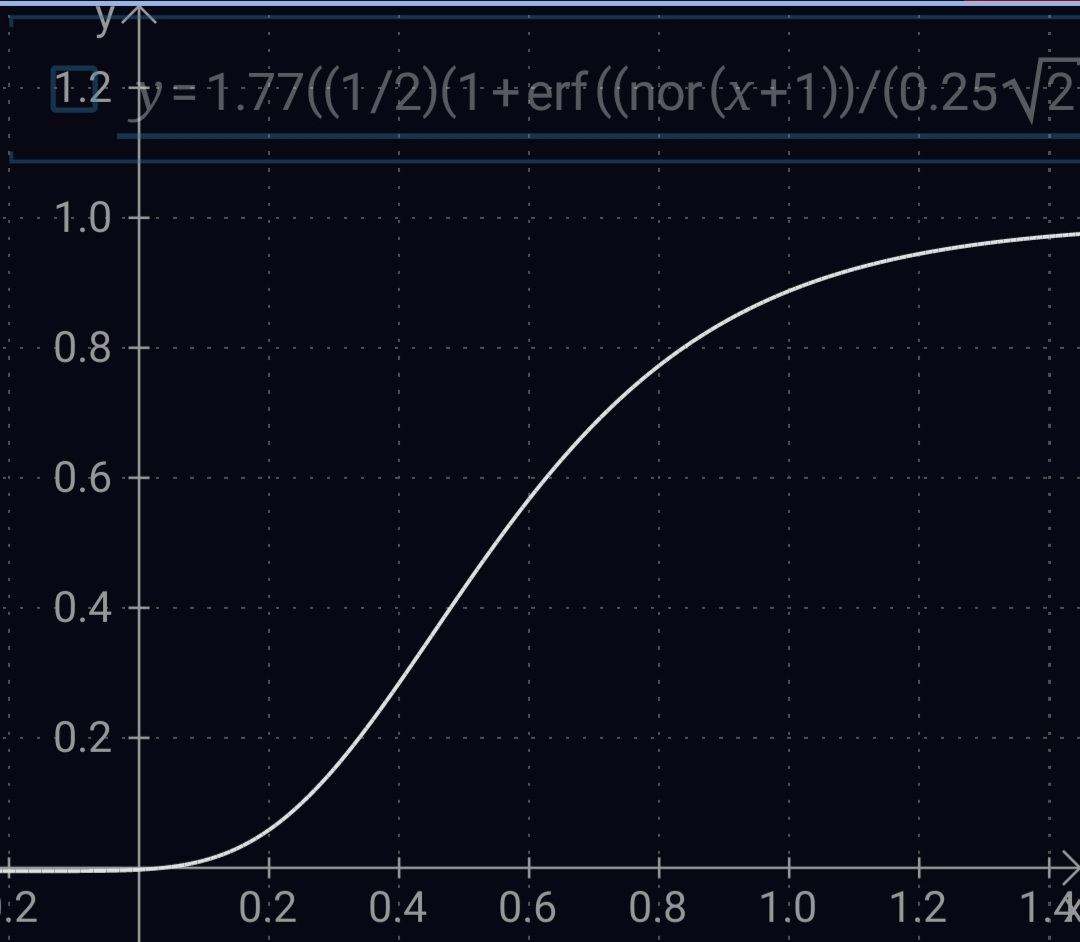
Edit: In case you're not looking for output similar to the distribution histogram that you provided and instead want something more similar to the sigmoid function you drew I have created an alternate version.

Thanks to Ruzihm for pointing this out.

I went ahead and used the CDF for the normal distribution: where erf is defined as the error function: . I added a coefficient of 1.77 to scale the output to keep it within 0d - 1d.

It should produce numbers similar to this:

Here you can find the alternate class:

public class DistributedRandom : Random
{
    public double Mean { get; set; } = 0.7d;

    private const double xOffset = 1d;
    private const double yOffset = 0.88d;
    private const double alpha = 0.25d;
    private readonly double sqrtOf2Pi = Math.Sqrt(2 * Math.PI);
    private readonly double leadingCoefficient;
    private const double cdfLimit = 1.77d;
    private readonly double sqrt2 = Math.Sqrt(2);
    private readonly double sqrtPi = Math.Sqrt(Math.PI);
    private readonly double errorFunctionCoefficient;
    private readonly double cdfDivisor;

    public DistributedRandom()
    {
        leadingCoefficient = 1d / (alpha * sqrtOf2Pi);
        errorFunctionCoefficient = 2d / sqrtPi;
        cdfDivisor = alpha * sqrt2;
    }

    public override double NextDouble()
    {
        double x = base.NextDouble();

        return CDF(x) - yOffset;
    }

    private double DistributionFunction(double x)
    {
        double exponent = -0.5d * Math.Pow((x - Mean) / alpha, 2d);

        double result = leadingCoefficient * Math.Pow(Math.E, exponent);

        return result;
    }

    private double ErrorFunction(double x)
    {
        return errorFunctionCoefficient * Math.Pow(Math.E,-Math.Pow(x,2));
    }

    private double CDF(double x)
    {
        x = DistributionFunction(x   xOffset)/cdfDivisor;

        double result = 0.5d * (1   ErrorFunction(x));

        return cdfLimit * result;
    }
}

CodePudding user response：

I came up with a workable solution. This isn't quite as elegant as I was aiming for because it requires 2 random numbers per result, but it definitely fulfills the requirement. Basically it takes one random number, uses another random number that's exponentially curved towards 1, and lerps towards the target.

I wrote it out in python because it was easier for me to visualize the histogram of it:

import math
import random

# Linearly interpolate between a and b by t.
def lerp(a, b, t):
    return ((1.0 - t) * a)   (t * b)

# What we want the median value to be.
target = 0.7
# How often we will hit that median value. (0 = uniform distribution, higher = greater chance of hitting median)
strength = 1.0

values = []
for i in range(0, 1000):
    # Start with a base float between 0 and 1.
    base = random.random()

    # Get another float between 0 and 1, that trends towards 1 with a higher strength value.
    adjust = random.random()
    adjust = 1.0 - math.pow(1.0 - adjust, strength)

    # Lerp the base float towards the target by the adjust amount.
    value = lerp(base, target, adjust)

    values.append(value)

# Graph histogram
import matplotlib.pyplot as plt
import scipy.special as sps
count, bins, ignored = plt.hist(values, 50, density=True)
plt.show()

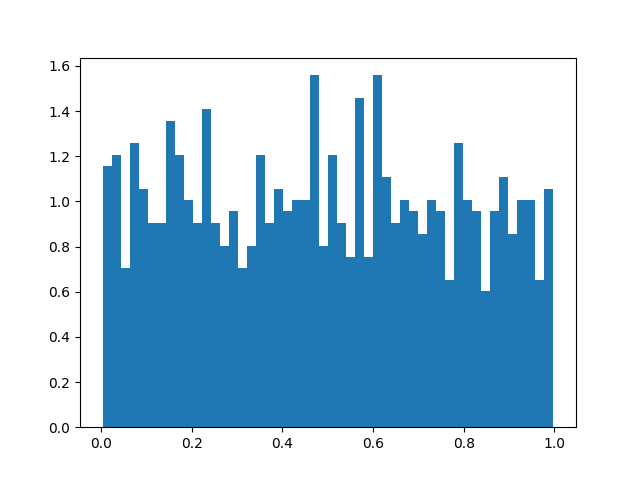
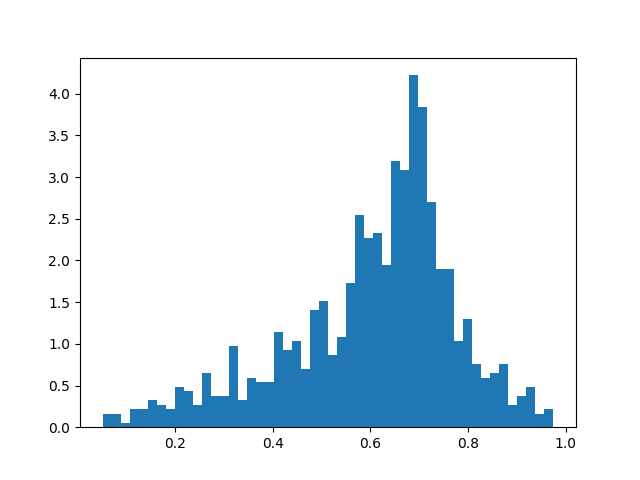
Target = 0.7, Strength = 1

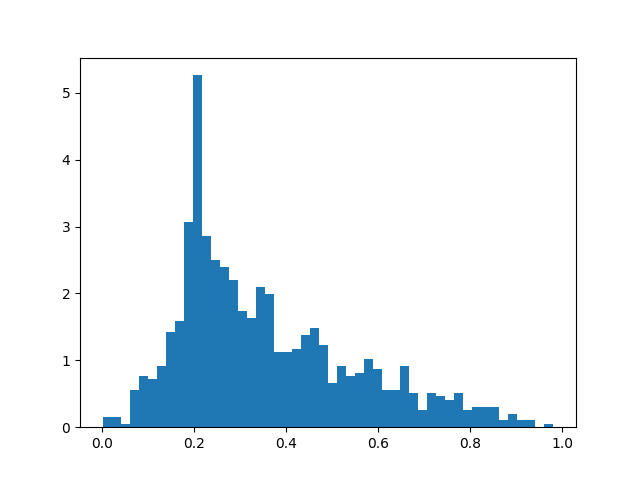
Target = 0.2, Strength = 1

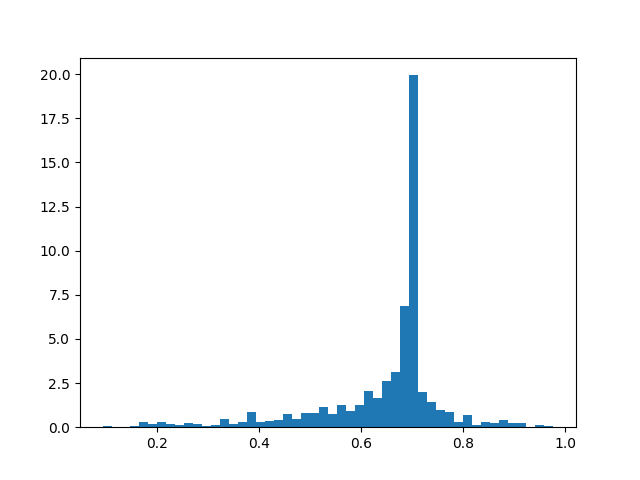
Target = 0.7, Strength = 3

Target = 0.7, Strength = 0

(This is meant to be uniform distribution - it might look kinda jagged, but I tested and that's just python's random number generator.)