I'm trying to write a matrix that transforms between the local coordinates of a transformed rectangle on the screen and the viewport coordinates.

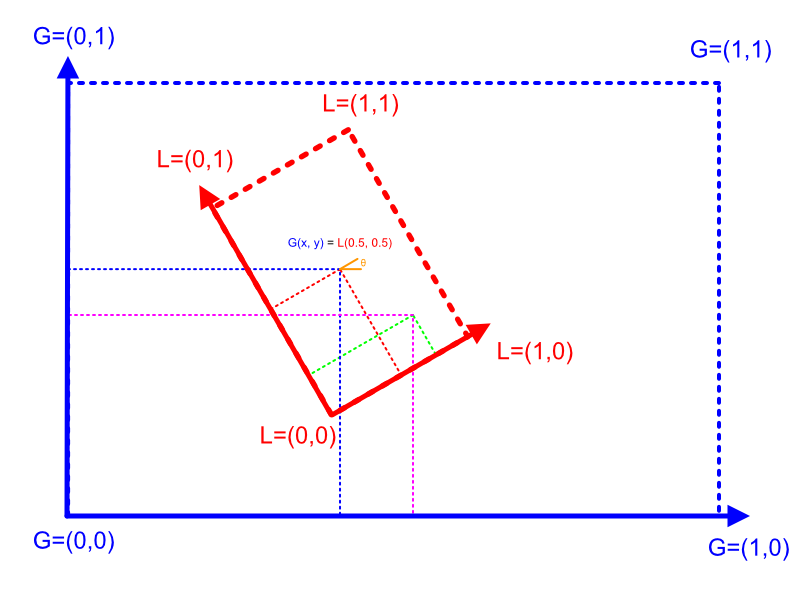
As illustrated in the following graph:

• The red local (L) coordinates represent the rectangle, from (0, 0) to (1, 1)
• The orange global (G) coordinates represent the viewport, from (0, 0) to (1, 1)
• The rectangle is centered at its (0.5, 0.5) coordinates, and rotated around that pivot by theta (orange)
• I'm trying to write a matrix that transforms the green local coordinates into the magenta global coordinates

So far, I have the following code, which works for translation and scaling, and seems to rotate in the right direction.

But there seems to be some form of skewing when rotation is applied:

public Matrix4x4 LocalToViewportMatrix
{
    get
    {
        Vector2 translation = viewportPosition;
        float rotation = this.rotation;
        Vector2 scale = viewportSize;
        Vector2 centering = -(new Vector2(0.5f, 0.5f));
        
        Matrix4x4 T = Matrix4x4.Translate(translation.WithZ(0));
        Matrix4x4 R = Matrix4x4.Rotate(Quaternion.Euler(0, 0, rotation));
        Matrix4x4 S = Matrix4x4.Scale(scale.WithZ(1));
        Matrix4x4 t = Matrix4x4.Translate(centering.WithZ(0));

        return T * R * S * t;
    }
}

• viewportPosition maps to the blue G(x, y) rectangle center on the graph
• rotation maps to the orange theta angle on the graph
• viewportSize maps to the relative size of the unrotated rectangle compared to the viewport; basically if you took length(red axes) / length(blue axes)

I'm pretty sure this has something to do with my order of operations, but I tried many things and can't figure it out.

CodePudding user response：

I managed to solve my issue by using absolute pixel coordinates for the viewport instead of a relative [0, 1] range. I'm not exactly sure how to explain it, but I think the fact that the coordinate system was not of the same length on both axes introduced the skewing.

public Matrix4x4 LocalToScreenMatrix
{
    get
    {
        var ScreenSize = new Vector2(Screen.width, Screen.height);
        var screenPosition = viewportPosition * ScreenSize;
        var screenSize = viewportSize * ScreenSize;

        var translation = screenPosition;
        var rotation = this.rotation;
        var scale = screenSize;
        var centering = -new Vector2(0.5f, 0.5f);

        var T = Matrix4x4.Translate(translation.WithZ(0));
        var R = Matrix4x4.Rotate(Quaternion.Euler(0, 0, rotation));
        var S = Matrix4x4.Scale(scale.WithZ(1));
        var t = Matrix4x4.Translate(centering.WithZ(0));

        return T * R * S * t;
    }
}