Let X,Y,Z,W be words with vector frequency $(x,y,z,w)$ , Find an op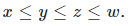timal code-CodePudding

Let X,Y,Z,W be words with vector frequency (x,y,z,w) such that $x\leq y\leq z\leq w$ .

Find certain requirements about x,y,z,w such that W=00,Z=01,Y=10,X=11 is an optimal code.

My solution :

Using Huffman coding, I think the solution is to demand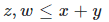

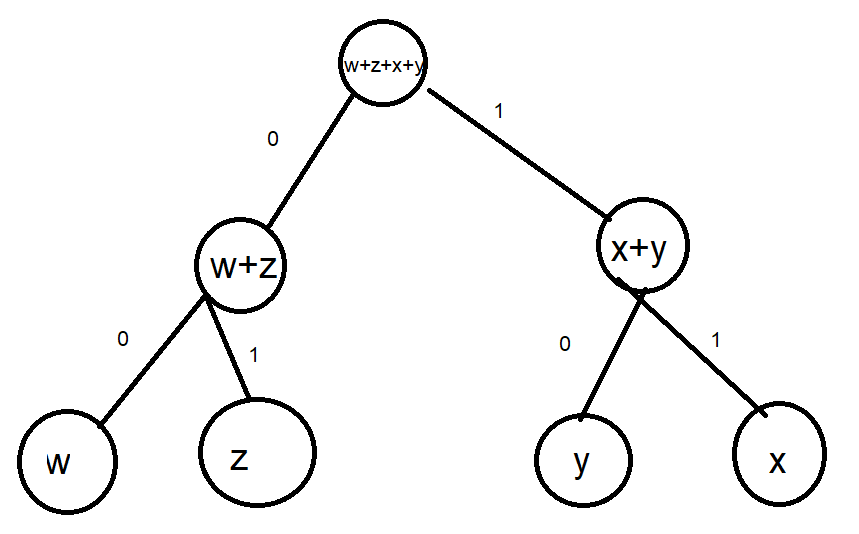
The tree is :

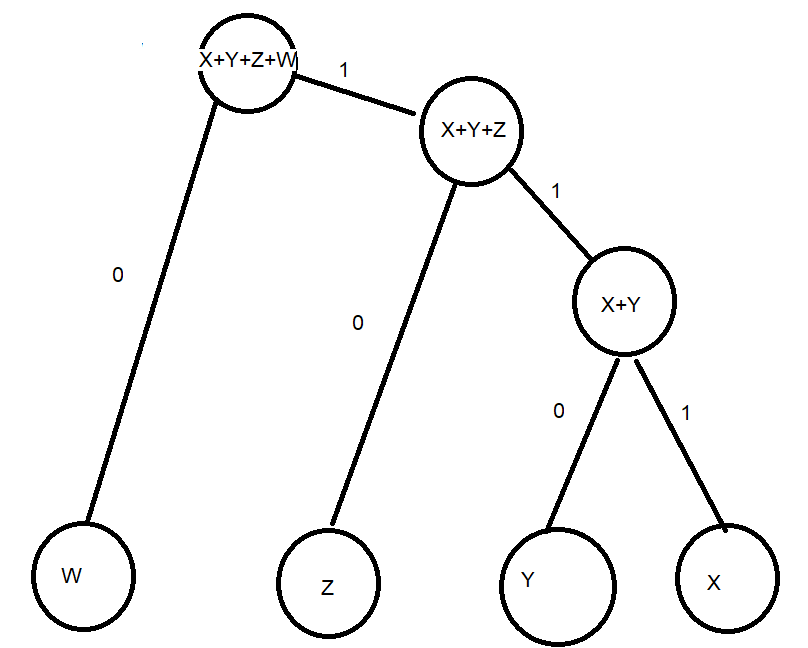
In a case that 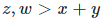the next tree is the appropriate tree:

Therefore the optimal code is W=0,Z=10,Y=110,X=111.

The optimal codes for both cases are correct?

Thanks !

CodePudding user response：

As noted in a comment to an answer here, specifically you need w ≤ x y in order for the top prefix code to be optimal. (The notation "z, w ≤ x y" has no conventionally accepted meaning, and z doesn't matter anyway, since its relation to w, x, and y is already given.) In the case of w = x y, then both of the prefix codes you show are optimal, and a properly implemented Huffman algorithm could produce either one. If w > x y, then the second code is optimal.

Another condition that was not given, but should have been, is x > 0. If x = 0 but y > 0, then x would not be coded at all, and there would be three symbols in the tree instead of four.

The trees you show are the only two possible prefix code topologies for four symbols.

CodePudding user response：

Your solution is correct and you can prove it as follows. First, argue that by requiring that both z and w be no greater than x y, that you can get an optimal code that looks like the one suggested; then, argue that if either z or w is greater than x y, you cannot get the code shown in any case.

As you point out clearly, when z and w are no greater than x y, you can get a balanced binary tree where ever symbol has a code of length two. One assignment of labels to edges gives the code shown.

Similarly, if either z or w is greater than x y, then Huffman will combine the node or x y with some other node before getting to the root; this means there will be paths of length at least three from the root to some leaves, so any code obtained by relabeling edges will have some codewords of length at least three. This cannot look like the code provided whose codewords are all of equal length two.