Finding a graph based algorithm to clean a room with some robots in the shortest time. The map/maze-CodePudding

I need help solving the following problem:

Given a room (matrix), where each square can be: a dirty spot that needs to be cleaned, an empty spot, a wall, or a starting position for a robot, I need to find the fastest way my robot network can clean the room. I must only print the time (number of squares passed by the longest running robot until all dirty spots are visited/cleaned).

The tile where the robot started from and the cleaned square will also act like normal squares, without any constraints. 2 robots can pass by the same empty tile at the same time (no crashing case), robots only "interact" to choose where to go, not physically.

Test cases accept maximum 4 robots, but the matrix can reach 1000x1000, and you can reach any part of the room with any robot.

Robot can move in the 4 directions as long as there is no wall in the next cell.

I know I have to use graphs and I believe backtracking will be an undesired solution and it will most likely not meet the time constraints, i am looking for a smarter solution.

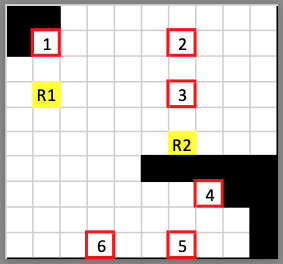
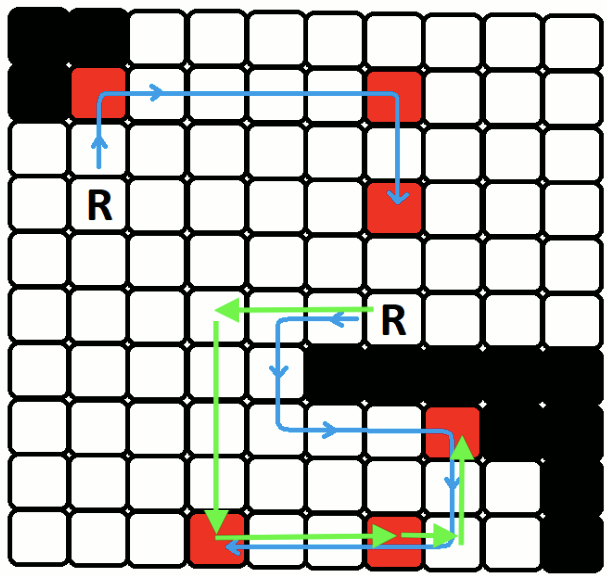
I will post the given examples, should be a lot easier to understand, the red spots are dirty and need to be reached:

Maze1

In this example the robot that goes up need 9 seconds to finish his route while the one that goes down needs 13 seconds so the answer is 13.

Maze2

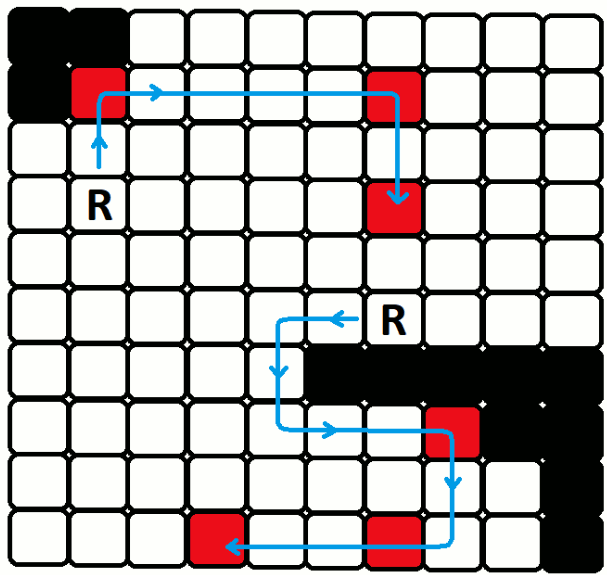
In the second picture the answer is 11, how much the robot "in the middle" requires to reach it's assigned spot.

CodePudding user response：

Add every square that is not a wall as a vertex to to your favorite graph theory library
Add an undirected edge between every adjacent square
Assign every red square to the nearest robot. On first pass use Pythagorean distance. Later take into account walls by using the A* algorithm.
Calculate best path for each robot to reach its assigned squares using the travelling salesman algorithm.
Output length of longest path.

Note that this will give a feasible answer, but not the optimum. For example, in your first example the red square in the 4th row ( 1-based ) will be assigned to the robot in the 6th row, instead of to the one in the 4th.

CodePudding user response：

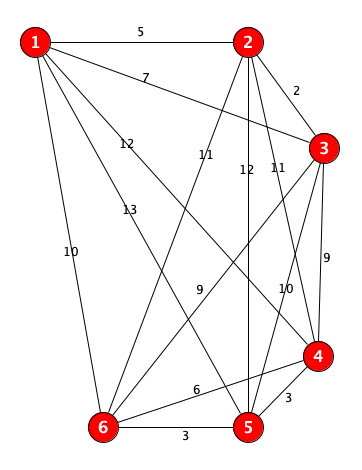
Step 1: prepare a base graph for all your dirty squares (named DirtyGraph):

All dirty squares becomes a node in your graph;
Construct a fully connected graph with edge weight equals to the steps between dirty squares;

Example:

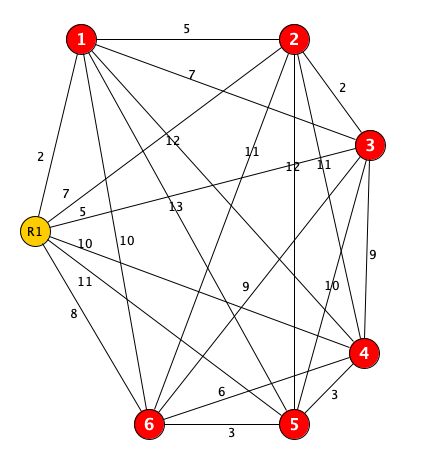
Step 2: for each Robot, clone DirtyGraph, add the robot as a new node to this graph, calculate and add all edges to this cloned graph so it's still a fully connected graph. Name these graph Robot1G, Robot2G, etc.

Example:

Step 3: Generate all combinations of partitioning the dirty nodes into N partitions, where N is the number of robots.

Example: 2 robots:

  1 | 2 3 4 5 6
  2 | 1 3 4 5 6
  3 | 1 2 4 5 6
  4 | 1 2 3 5 6
  5 | 1 2 3 4 6
  6 | 1 2 3 4 5
  1 2 | 3 4 5 6
  1 3 | 2 4 5 6
  1 4 | 2 3 5 6
  1 5 | 2 3 4 6
  1 6 | 2 3 4 5
  2 3 | 1 4 5 6
  2 4 | 1 3 5 6
  .....

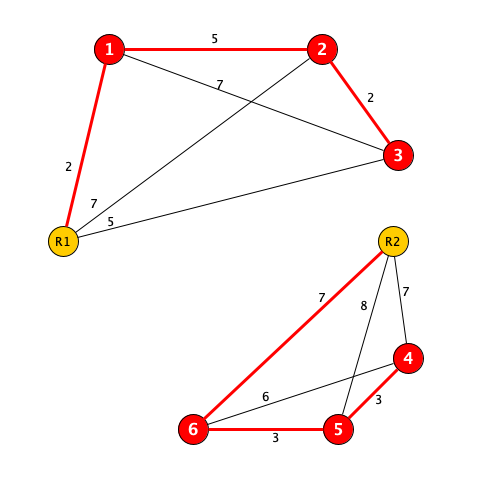
Step 4, for each combination of partition, assign the partitions to all combinations of robots, extract sub-graph from Robot?G and solve it as a Traveling Salesman Problem (TSP). With an "answer" you got the time for each robot to complete its own partition of dirty nodes.

Example: Partition 1 2 3 for R1 and 4 5 6 for R2

max() of time required for all robots in their own partition BECOMES the "time required for THIS combination of partition".

Step 5, after you calculation all combinations of partitions, the partition combination uses the minimal time will be the ANSWER you want, and the TSP results of the robot sub-graphs of (ANSWER) is the robot path.

This is also an answer:

Let's burn the CPU for the "correct" BEST path!