Now I want to calculate the area under the curve from x = 0 to x = 0.6. When I look for appropriate packages I only find something like calculation AUC of a ROC curve. But is there a way just to calculate the AUC of a normal function?
CodePudding user response:
The area under the curve (AUC) of a given set of data points can be archived using numeric integration:
Let data be your data frame containing x and y values. You can get the area under the curve from lower x0=0 to upper x1=0.6 by integrating the function, which is linearly approximating your data.
This is a numeric approximation and not exact, because we do not have an infinite number of data points: For y=sqrt(x) we will get 0.3033 instead of true value of 0.3098. For 200 rows in data we'll get even better with auc=0.3096.
library(tidyverse)
data <-
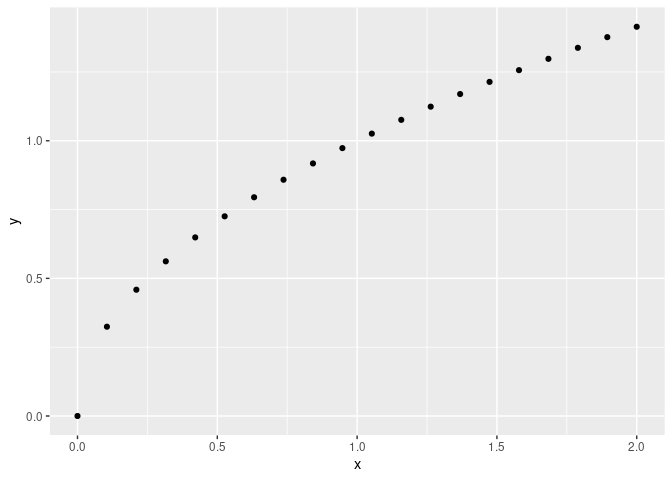
tibble(
x = seq(0, 2, length.out = 20)
) %>%
mutate(y = sqrt(x))
data
qplot(x, y, data = data)
integrate(approxfun(data$x, data$y), 0, 0.6)
Created on 2021-10-03 by the reprex package (v2.0.1)
The absolute error returned by integrate is corerect, iff the real world between every two data points is a perfect linear interpolation, as we assumed.
CodePudding user response:
I used the package MESS to solve the problem:
library(MESS)
x <- seq(0,3, by=0.1)
y <- x^2
auc(x,y, from = 0.1, to = 2, type = "spline")
The analytical result is:
7999/3000
Which is approximately 2.666333333333333
The R script offered gives: 2.66632 using the spline approximation and 2.6695 using the linear approximation.

