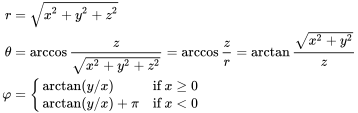Converting spherical coordinates into Cartesian and then converting back into Cartesian isn't g-CodePudding

I'm trying to write two functions for converting Cartesian coordinates to spherical coordinates and vice-versa. Here are the equations that I've used for the conversions (also could be found on this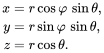

And

Here is my spherical_to_cartesian function:

def spherical_to_cartesian(theta, phi):
    x = math.cos(phi) * math.sin(theta)
    y = math.sin(phi) * math.sin(theta)
    z = math.cos(theta)
    return x, y, z

Here is my cartesian_to_spherical function:

def cartesian_to_spherical(x, y, z):
    theta = math.atan2(math.sqrt(x ** 2   y ** 2), z)
    phi = math.atan2(y, x) if x >= 0 else math.atan2(y, x)   math.pi
    return theta, phi

And, here is the driver code:

>>> t, p = 27.500, 7.500
>>> x, y, z = spherical_to_cartesian(t, p)
>>> print(f"Cartesian coordinates:\tx={x}\ty={y}\tz={z}")
Cartesian coordinates:  x=0.24238129061573832   y=0.6558871334524494    z=-0.7148869687796651
>>> theta, phi = cartesian_to_spherical(x, y, z)
>>> print(f"Spherical coordinates:\ttheta={theta}\tphi={phi}")
Spherical coordinates:  theta=2.367258771281654 phi=1.2168146928204135

I can't figure out why I'm getting different values for theta and phi than my initial values (the output values aren't even close to the input values). Did I make a mistake in my code which I can't see?

CodePudding user response：

You seem to be giving your angles in degrees, while all trigonometric functions expect radians. Multiply degrees with math.pi/180 to get radians, and multiply radians with 180/math.pi to get degrees.

CodePudding user response：

The results are correct, but you should check their value using the modulo pi operation.

Trigonometric functions in the math package expect the input angles in radians. This means that your angles are larger than 2*pi and are equivalent to any other value obtained by adding or subtracting 2*pi (which also represents a full rotation in radians).

In particular you have that:

>>> 27.5 % (2*math.pi)
2.367258771281655

>>> 7.500 % (2*math.pi)
1.2168146928204138