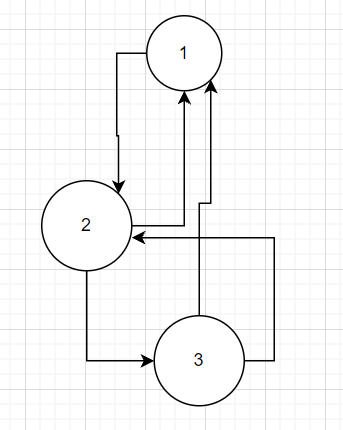
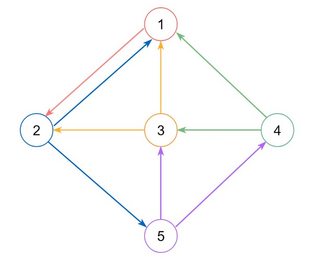
Given a graph below, find all the possible path from vertex 1 to come back to 1 including back edges.
Result:
[1,2,3,2,1]
[1,2,1]
[1,2,3,1]
I tried using DFS able to get only one cycle [1,2,3,2,1]. I'm not getting how to get track of back edges.
Code:
private static void dfsNow(Node vertex, HashMap<String, List<Node>> adjList,
HashSet<String> visited, HashSet<String> candidates,
ArrayList<String> res) {
candidates.add(vertex.v);
res.add(vertex.v);
for(Node adj : adjList.get(vertex.v)) {
if(candidates.contains(adj.v)) {
res.add(adj.v);
System.out.println(vertex.v ":" adj.v);
} else {
//adj.setParent(vertex); // build the trace back
dfsNow( adj, adjList,visited,candidates,res);
}
}
candidates.remove(vertex.v);
visited.add(vertex.v);
}
CodePudding user response:
You were close to the answer.
In order to detect a cycle in a graph, you need to use the Depth first search algorithm. That's correct.
But there are a couple of things in your solution that has to improved:
- For this task, you don't need edges. Because you can model a directed graph by using vertices only. Edges are useful when you deal with a weighted graph (i.e. every edge is associated with a value) and need to address, for instance, the problem of the shortest path using Dijkstra's or Bellman–Ford algorithms. Then you really need edges to model the connections between vertices. But for in this task, edges are redundant, each vertex can point to other vertexes.
- Adjacency list mustn't be a separate data structure. Instead, every vertex has to be aware of its neighbors. I.e. each vertex must hold a reference to a collection of adjacent vertices.
- Since graph can contain multiple cycles, the result need to be represented by the nested collection. Like list of lists
List<List<Vertex>>. contains()checks done on aListare very costful (O(n) in the worse case), and isn't list capable to associate elements.Mapis a better choice because map allow to retrieve values in a constant time and associate multiple keys with the same value (i.e. model cases when a group of vertices points is being connected with a single vertex).
Note that cycle [1,2,3,2,1] isn't valid because there's more than one vertex that was visited twice. It's a combination of two cycles 1-2 and 2-3. If you need to spot all the cycles in a graph they must be detected only one at a time, otherwise attempt to restore the path of a cycle might fail because of references pointing one at each other. Only because in your solution is capable to track only a single path, you didn't run in to trouble with the second cycle 2->3->2. I.e. all vertexes (except one) in a cycle must be unique, that will allow to maintain multiple paths.
In the implementation below, I deliberately provided a method that is able to detect cycles that contain a particular vertex, as well a method that fetches all the cycles comprised of only unique vertices. So that you can play around by changing them and make sure that map should never contain the last segment of cycle. I.e. only entry 2->3 will be added by into map, but entry 3->2 will not, otherwise you can create an infinite loop.
Implementation of the graph below utilizes only vertexes. Depth first search algorithm is implemented iteratively (although recursive implementation is easier, recursion has limitation in Java especially when dealing with a large dataset and iterative approach is more performant).
public class CyclicGraph {
private Map<Integer, Vertex> vertexById = new HashMap<>();
public void addVertex(int vertexId, int... neighbours) {
// vertexById.putIfAbsent(vertexId, new Vertex(vertexId));
// Vertex current = vertexById.get(vertexId); // does the same as the line below with one important distinction - new Vertex will be instantiated by `computeIfAbsent` only entry is not present
Vertex current = vertexById.computeIfAbsent(vertexId, Vertex::new); // adding a vertex
for (int next : neighbours) {
Vertex neighbour = vertexById.computeIfAbsent(next, Vertex::new); // retrieving neighbour
current.addNeighbour(neighbour); // adding neighbour
}
}
public List<List<Vertex>> getCyclesContainingVertex(int targetId) {
Vertex target = vertexById.get(targetId);
if (vertexById.get(targetId) == null) {
return Collections.emptyList();
}
List<List<Vertex>> cycles = new ArrayList<>();
Deque<Vertex> stack = new ArrayDeque<>();
Set<Vertex> seen = new HashSet<>();
Map<Vertex, Vertex> paths = new HashMap<>();
stack.add(target);
while (!stack.isEmpty()) {
Vertex current = stack.pop();
seen.add(current);
for (Vertex neighbour : current.getNeighbours()) {
if (seen.contains(neighbour) && neighbour.equals(target)) { // the cycle was found
// build cycle, don't add vertex to the stack and don't add new entry to the paths (it can prevent other cycles containing neighbour vertex from being detected)
cycles.add(buildCycle(paths, neighbour, current));
} else if (!seen.contains(neighbour)) {
stack.add(neighbour);
paths.put(neighbour, current);
seen.add(neighbour);
}
}
}
return cycles;
}
public List<List<Vertex>> getAllCycles() {
List<List<Vertex>> cycles = new ArrayList<>();
Deque<Vertex> stack = new ArrayDeque<>();
Set<Vertex> seen = new HashSet<>();
for (Vertex next : vertexById.values()) {
if (seen.contains(next)) continue;
Map<Vertex, Vertex> paths = new HashMap<>();
stack.add(next);
while (!stack.isEmpty()) {
Vertex current = stack.pop();
seen.add(current);
for (Vertex neighbour : current.getNeighbours()) {
if (seen.contains(neighbour)) { // the cycle was found
// build cycle, don't add vertex to the stack and don't add new entry to the paths (it can prevent other cycles containing neighbour vertex from being detected)
cycles.add(buildCycle(paths, neighbour, current));
} else {
stack.add(neighbour);
paths.put(neighbour, current);
seen.add(neighbour);
}
}
}
}
return cycles;
}
private List<Vertex> buildCycle(Map<Vertex, Vertex> paths, Vertex start, Vertex end) {
Deque<Vertex> cycle = new ArrayDeque<>();
Vertex current = end;
while (current != null && !current.equals(start)) {
cycle.addFirst(current);
current = paths.get(current);
}
cycle.addFirst(start);
return new ArrayList<>(cycle);
}
public void clear() {
this.vertexById.clear();
}
private class Vertex {
private int id;
private Set<Vertex> neighbours = new HashSet<>();
public Vertex(int id) {
this.id = id;
}
public boolean addNeighbour(Vertex vert) {
return neighbours.add(vert);
}
// getters, hashCode/equeals, toString()
}
}
Example of a bit more elaborate graph used in demo together with the graph provided in the question.
main() - demo
public static void main(String[] args) {
CyclicGraph graph = new CyclicGraph();
System.out.println("Graph described in the question (only cycles that include vertex 1):");
graph.addVertex(1, 2);
graph.addVertex(2, 1, 3);
graph.addVertex(3, 1, 2);
for (List<Vertex> cycle : graph.getCyclesContainingVertex(1)) {
System.out.println(cycle);
}
graph.clear();
System.out.println("\nMore elaborate Graph (all cycles):");
graph.addVertex(1, 2);
graph.addVertex(2, 1, 5);
graph.addVertex(3, 1, 2);
graph.addVertex(4, 1, 3);
graph.addVertex(5, 3, 4);
for (List<Vertex> cycle : graph.getAllCycles()) {
System.out.println(cycle);
}
}
Output
Graph described in the question (cycles that lead to 1):
[Vertex{ 1 }, Vertex{ 2 }] // 1 is reachable from 2
[Vertex{ 1 }, Vertex{ 2 }, Vertex{ 3 }] // 1 is reachable from 3
More elaborate Graph (all cycles):
[Vertex{ 1 }, Vertex{ 2 }] // 1 is reachable from 2
[Vertex{ 2 }, Vertex{ 5 }, Vertex{ 3 }] // 2 is reachable from 3
[Vertex{ 1 }, Vertex{ 2 }, Vertex{ 5 }, Vertex{ 3 }] // 1 is reachable from 3
[Vertex{ 3 }, Vertex{ 1 }, Vertex{ 2 }, Vertex{ 5 }, Vertex{ 4 }] // 3 is reachable from 4
[Vertex{ 1 }, Vertex{ 2 }, Vertex{ 5 }, Vertex{ 4 }] // 1 is reachable from 4