How to solve exponential equation with two variables?-CodePudding

Background

I have one exponential equation like this:

a - b * np.exp(-c/x) - y * np.exp(-delta/x).sum() * 2

where a, b, and c are constants, the delta is a 1D array that is available from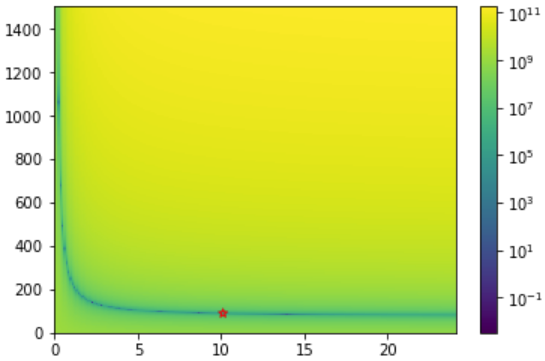

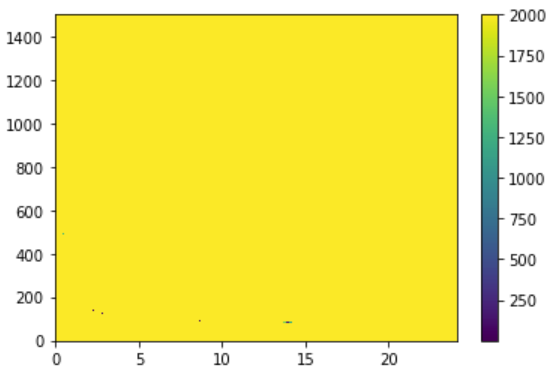
Here's the same data with lower vmax:

m = ax.pcolormesh(X, Y, (res**2).T, cmap='viridis', vmax=2e3)

CodePudding user response：

Your equation looks like this:

a - b * np.exp(-c/x) - y * np.exp(-delta/x).sum() * 2 = 0

Which is to say:

y = (a - b * np.exp(-c/x)) / np.exp(-delta/x).sum() / 2

You can plug any value for x and get the corresponding y:

>>> import numpy as np; import matplotlib.pyplot as plt
>>> a,b,c = 35167.7, 11919.5, 1.68
>>> delta  = np.load('delta.npy')
>>> def the_y(x): return (a - b * np.exp(-c/x)) / np.exp(-delta/x).sum() / 2
... 
>>> import matplotlib.pyplot as plt
>>> X = np.linspace(1, 24, 1000)
>>> plt.plot(X, [the_y(x) for x in X]); plt.show()

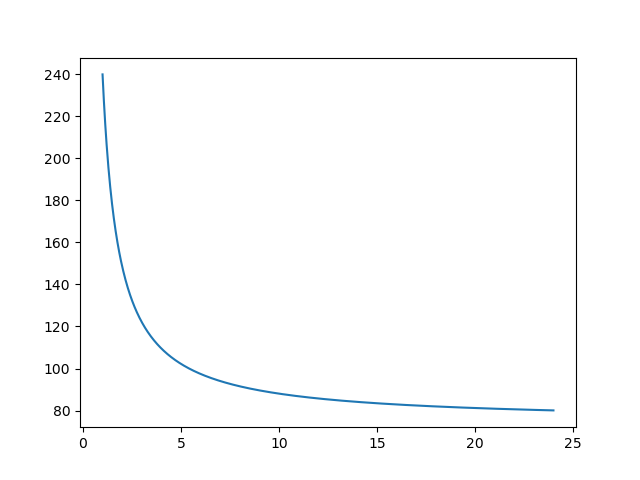
Here's the plot:

Indeed, for each x in X = np.linspace(1, 24, 1000) I got the corresponding y value. You could generate a bazillion of xs and get a bazillion of ys in response, so I'd say there are infinitely many solutions.