How to get a better approximation of a thick bezier curve?-CodePudding

Let's say I already have a bezier curve approximated by many straight lines (the bezier array in the code), and I would like to draw it with a series of rectangles. I have the following code below that does exactly this:

// don't change this array
const bezier = [{x:167.00,y:40.00},{x:154.37,y:42.09},{x:143.09,y:44.48},{x:133.08,y:47.15},{x:124.26,y:50.09},{x:116.55,y:53.27},{x:109.87,y:56.68},{x:104.15,y:60.31},{x:99.32,y:64.14},{x:95.28,y:68.15},{x:91.97,y:72.34},{x:89.31,y:76.67},{x:87.22,y:81.14},{x:85.63,y:85.74},{x:84.44,y:90.43},{x:83.60,y:95.22},{x:83.02,y:100.08},{x:82.63,y:105.00},{x:82.33,y:109.96},{x:82.07,y:114.94},{x:81.76,y:119.94},{x:81.33,y:124.93},{x:80.69,y:129.89},{x:79.77,y:134.82},{x:78.49,y:139.70},{x:76.78,y:144.50},{x:74.55,y:149.22},{x:71.74,y:153.84},{x:68.25,y:158.34},{x:64.03,y:162.71},{x:58.97,y:166.93},{x:53.02,y:170.98},{x:46.10,y:174.86},{x:38.11,y:178.54},{x:29.00,y:182.00}];

const canvas = document.querySelector("canvas");
const ctx = canvas.getContext("2d");

const thickness = 35;

function rotateCanvas(x, y, a) {
  ctx.translate(x, y);
  ctx.rotate(a);
  ctx.translate(-x, -y);
}

function drawRectangle(rX, rY, rW, rH, rA, color) {
  ctx.beginPath();
  rotateCanvas(rX   rW / 2, rY   rH / 2, rA);
  ctx.rect(rX, rY, rW, rH);
  rotateCanvas(rX   rW / 2, rY   rH / 2, -rA);
  ctx.fill();
}

function calcRectFromLine(x1, y1, x2, y2) {
  const dx = x2 - x1;
  const dy = y2 - y1;
  const mag = Math.sqrt(dx * dx   dy * dy);
  const angle = Math.atan2(dy, dx);

  return { 
    x: (x1   x2) / 2 - mag / 2,
    y: (y1   y2) / 2 - thickness / 2,
    w: mag,
    h: thickness,
    a: angle
  };
}

function calculateRectangles() {
  const result = [];

  for (let i = 1; i < bezier.length; i  ) {
    const prev = bezier[i - 1];
    const curr = bezier[i];

    result.push(calcRectFromLine(prev.x, prev.y, curr.x, curr.y));
  }

  return result;
}

const rectangles = calculateRectangles();

for (let r of rectangles) {
  drawRectangle(r.x, r.y, r.w, r.h, r.a);
}

<canvas width="400" height="400"></canvas>

If you run the snippet you'll see that the curve is not fully thick, and the fact that it is a series of rectangles is very obvious.

If you change the thickness parameter from 35 to a lower number and re-run it, it looks fine. It's only when it's very thick does this occur.

The code currently takes the bezier array, and creates a series of rotated rectangles and then renders them.

Is there any way to modify the calculateRectangles function to return a better approximation of the curve? Ideally it would still return a list of rectangles rotated around their center, but when rendered it would look more like the curve, and less like a list of rectangles.

The only idea I could think of is to somehow return twice as many rectangles from calculateRectangles, where each one is inverted from the previous one, such that both sides of the line are filled in, and while I think that might work, it unfortunately has the side-effect of returning twice as many rectangles, which is undesirable and I would to avoid it if possible.

CodePudding user response：

The shapes that you should draw are not rectangles but quadrilaterals, obtained by joining the endpoints of the successive normals to the curve. Presumably, you can achieve that by means of Path objects.

In zones of high curvature, you may have to yet reduce the step, because the outer curve might not be smooth.

In fact, you can "flatten" a Bezier curve by choosing steps so that the deviation between successive segments remains bounded below a fixed tolerance.

In the case of a thick curve, you can keep that idea but making sure that the bounded deviation holds for both sides of the curve.

CodePudding user response：

you can't really make a "thick bezier" by drawing rectangles, you're just going to end up with lots of gaps between them on one size, and weird looking overlap on the other side. If you want to stick with the polygon approximation, you'll need to use the normal at each of your points, and then draw lines to connect those. This leads to trapezoidal sections, so we can't use plain rects if we want decent looking results.

However, the bigger the offset, the more you're going to have problems in areas with tiny radius of curvature: you can already see one such problem just by looking at the normals crossing each other underneath the crest in the upper left, where we don't actually want to connect all normal-offset vertices, because one of them lies inside the shape we want to trace.

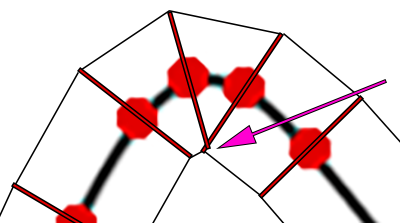
Alternatively, you can offset the bezier curve itself with "more beziers", e.g.