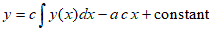I've been using this tutorial (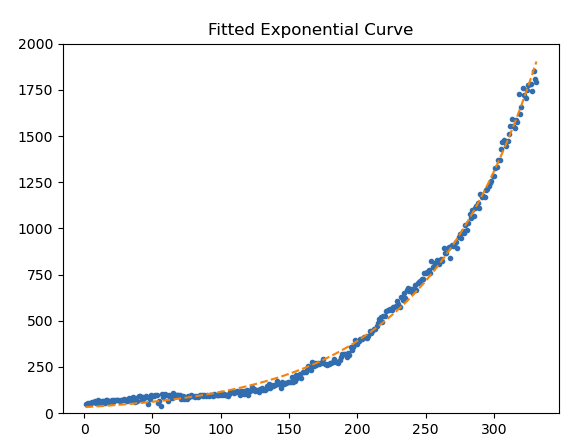

Finally I should add that I'd give it some more though if a least squares fit (which is what curve_fit uses) is really what you want for an exponential function, or whether there might be other alternatives to find a working approximation.

CodePudding user response：

The flawr's answer is very good. In fact there is no need for more answers.

Nevertheless I would like to add a comment (too long to be edited in the comments section).

The method of nonlinear regression used in your sofware is iterative. It is well known that starting the iterative calculus requiers to set some initial values to the parameters. That is judiciously mentioned in the flawr's answer with an empirical approach to guess initial values.

This is very important because if the initial values are too far from the unknown correct values the iterative calculus might fail.

Of course all would be easier with a not iterative method which doesn't require to guess initial values. Such a method exists as shown below.

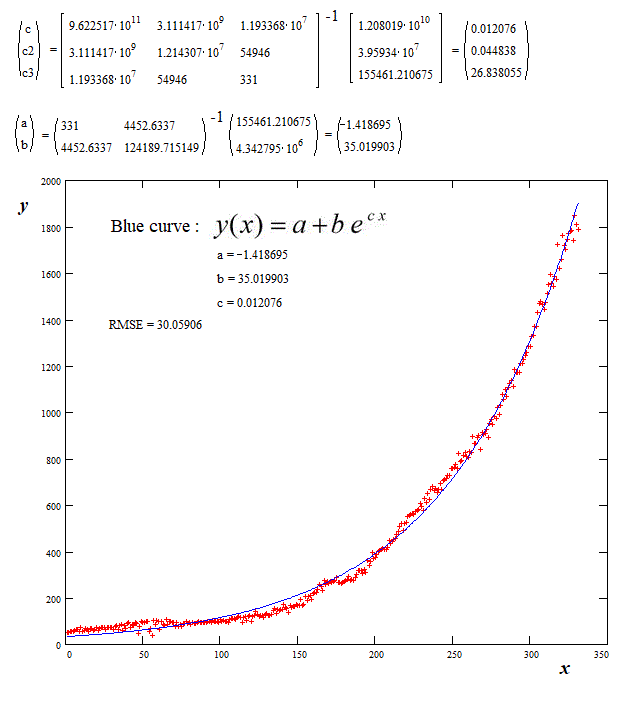
Numerical example with your data :

Comparing to non linear regression (iterative method) one obtain :

a=-2.91212 ; b=35.547425 ; c=0.012030 ; RMSE=30.050141 (Root Mean Square Error).

With this data the fitting is the same for the both methods. One cannot distinguish any difference between the two respective blue curves on the above graph.

FOR INFORMATION :

The above method is a linear regression wrt a linear integral equation to which the exponential equation is solution :

In the numerical calculus the Sk are the values of the integral computed by numerical integration.

Ref.: https://fr.scribd.com/doc/14674814/Regressions-et-equations-integrales