The Matplotlib Result is Different From WolfarmAlpha-CodePudding

I want to plot some equation in Matplotlib. But it has different result from Wolframalpha.

This is the equation:

y = 10yt y^2t 20

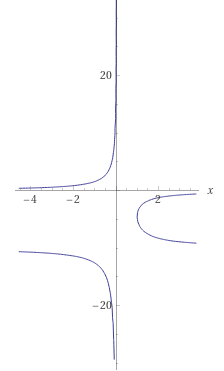
The plot result in wolframalpha is:

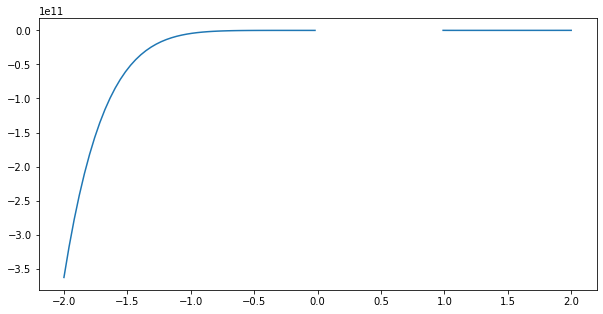
But when I want to plot it in the matplotlib with these code

# Creating vectors X and Y
x = np.linspace(-2, 2, 100)
# Assuming α is 10
y = ((10*y*x) ((y**2)*x) 20)
# Create the plot
fig = plt.figure(figsize = (10, 5))
plt.plot(x, y)

The result is:

Any suggestion to modify to code so it has similar plot result as wolframalpha? Thank you

CodePudding user response：

As @Him has suggested in the comments, y = ((10*y*x) ((y**2)*x) 20) won't describe a relationship, so much as make an assignment, so the fact that y appears on both sides of the equation makes this difficult.

It's not trivial to express y cleanly in terms of x, but it's relatively easy to express x in terms of y, and then graph that relationship, like so:

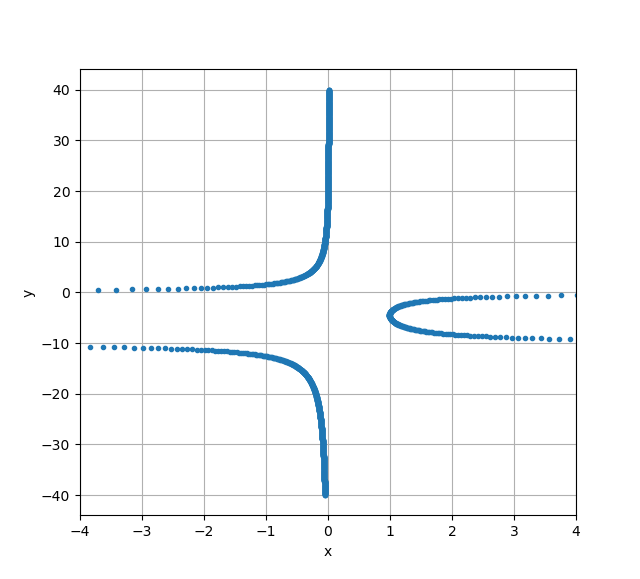
import numpy as np
import matplotlib.pyplot as plt

y = np.linspace(-40, 40, 2000)

x = (y-20)*(((10*y) (y**2))**-1)
fig, ax = plt.subplots()

ax.plot(x, y, linestyle = 'None', marker = '.')
ax.set_xlim(left = -4, right = 4)
ax.grid()
ax.set_xlabel('x')
ax.set_ylabel('y')

Which produces the following result:

If you tried to plot this with a line instead of points, you'll get a big discontinuity as the asymptotic limbs try to join up

So you'd have to define the same function and evaluate it in three different ranges and plot them all so you don't get any crossovers.

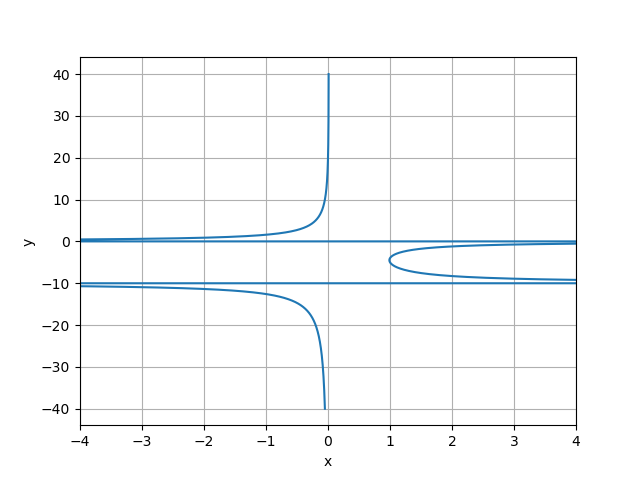
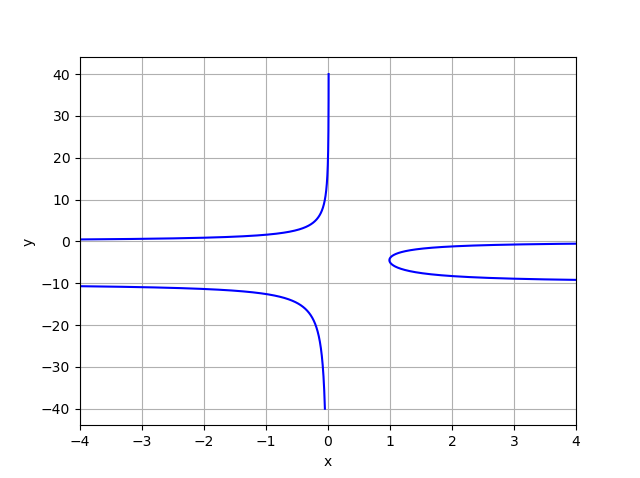
import numpy as np
import matplotlib.pyplot as plt

y1 = np.linspace(-40, -10, 2000)
y2 = np.linspace(-10, 0, 2000)
y3 = np.linspace(0, 40, 2000)

x = lambda y: (y-20)*(((10*y) (y**2))**-1)

y = np.hstack([y1, y2, y3])


fig, ax = plt.subplots()

ax.plot(x(y), y, linestyle = '-', color = 'b')

ax.set_xlim(left = -4, right = 4)
ax.grid()
ax.set_xlabel('x')
ax.set_ylabel('y')

Which produces this result, that you were after: