Area under the histogram is not 1 when using density in plt.hist-CodePudding

Consider the following dataset with random data:

test_dataset = np.array([ -2.09601881,  -4.26602684,   1.09105452,  -4.59559669,
         1.05865251,  -0.93076762, -14.70398945, -18.01937129,
         4.64126152, -10.34178822,  -9.46058493,  -5.66864965,
        -3.17562022,  15.7030379 ,  10.59675205,  -5.80882413,
       -24.00604149,  -4.81518663,  -1.94333927,   1.18142171,
        12.72030312,   3.84917581,  -0.4468796 ,  11.91828567,
       -17.99171774,   9.35108712,  -5.57233376,   5.77547128,
         5.49296099, -10.96132844, -18.75174336,   5.27843303,
        25.73548956, -21.58043021, -14.24734733,  12.57886018,
       -22.10002076,   1.72207555,  -6.0411867 ,  -3.63568527,
         7.26542117,  -0.21449529,  -6.64974714,  -0.94574606,
        -4.23339431,  16.76199734, -12.42195793,  18.965854  ,
       -23.85336123, -15.55104466,   6.17215868,   7.34993316,
         8.62461351, -16.30482638, -16.35601099,   1.96857833,
        18.74440399, -22.48374434, -10.895831  , -10.14393648,
       -17.62768751,   4.83388855,  20.1578181 ,   6.04299626,
         0.97198296,  -3.40889754, -10.62734293,   1.70240472,
        20.4203839 ,  10.26751364,  15.47859675, -10.97940064,
         1.82728251,   4.22894717,   8.31502887,  -5.48502811,
        -1.09244874, -11.32072796, -24.88520436,  -7.42108403,
        19.4200716 ,   4.82704045, -12.46290135, -15.18466755,
         6.37714692, -11.06825059,   5.10898588,  -9.07485484,
         1.63946084, -12.2270078 ,  12.63776832, -25.03916909,
         2.42972082, -14.22890171,  18.2199446 ,   6.9819771 ,
       -12.07795089,   2.59948596, -16.90206575,   6.35192719,
         7.33823106, -23.69653447, -11.66091871, -19.40251179,
       -12.64863792,  11.04004231,  13.7247356 , -16.36107329,
        20.43227515,  17.97334692,  16.92675175,  -5.62051239,
        -8.66304184,  -8.40848514, -23.20919855,   0.96808137,
        -5.03287253,  -3.13212582,  18.81155666,  -8.27988284,
         3.85708447,  12.43039322,  17.98003878,  18.11009997,
        -3.74294421, -16.62276121,   9.4446743 ,   2.2060981 ,
         8.34853736,  14.79144713,  -1.91113975,  -5.17061419,
         4.53451746,   8.19090358,   7.98343201,  11.44592322,
       -16.9132677 , -25.92554857,  10.10638432,  -8.09236786,
        20.8878207 ,  19.52368296,   0.85858125,   2.61760415,
         9.21360649,  -8.1192651 ,  -6.94829273,   2.73562447,
        13.40981323,  -9.05018331, -17.77563166, -21.03927199,
         4.10415845,  -1.31550732,   5.68284828,  15.08670773,
       -19.78675315,  12.94697869, -11.51797637,   1.91485992,
        16.69417993, -16.04271622,  -1.14028558,   9.79830109,
       -18.58386093,  -7.52963269, -10.10059878, -25.2194216 ,
        -0.10598426, -15.77641532, -14.15999125,  14.35011271,
        11.15178588, -14.43856266,  15.84015226,  -3.41221883,
        11.90724469,   0.57782081,  18.82127466,  -6.01068727,
       -19.83684476,   2.20091942,  -1.38707755,  -8.62821053,
       -11.89000913, -11.69539815,   5.70242019,  -3.83781841,
         5.35894135,  -0.30995954,  21.76661212,   8.52974329,
        -9.13065082, -11.06209   , -12.00654618,   2.769838  ,
       -12.21579496, -27.2686534 ,  -4.58538197,  -6.94388425])

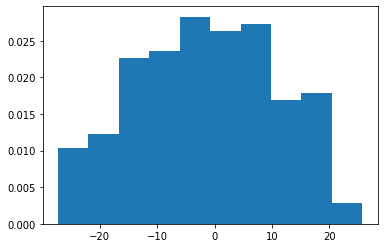
I'd like to plot normalized histogram of it, so in the plt.hist options I choose density=True:

import numpy as np
import matplotlib.pyplot as plt

data1, bins, _ = plt.hist(test_dataset, density=True);
print(np.trapz(data1))
print(sum(data1))

which outputs the following histogram:

0.18206124014272715

0.18866449755723017

From matplotlib documentation:

The density parameter, which normalizes bin heights so that the integral of the histogram is 1. The resulting histogram is an approximation of the probability density function.

But from my example it is clearly seen that the integral of the histogram is NOT 1 and strongly depends on the number of bins: if I specify it for example to be 40 the sum will increase:

data1, bins, _ = plt.hist(test_dataset, density=True);
print(np.trapz(data1))
print(sum(data1))

0.7508847002777762

0.7546579902289207

Is it incorrect description in documentation or I misunderstand some issues here?

CodePudding user response：

you do not calculate the area, area you should calculate as follow (in your example):

sum(data1 * np.diff(bins)) == 1