Uniroot function to find the inverse of a custom CDF then plotting a QQ function-CodePudding

I am trying to plot a qq function of a custom CDF function, of the form f(x)= p*e^-x (1-p)*e^-5x, p being between 0 and 1, and x greater than 0. Data has values 0<x<500,000

In doing this I have stumbled across the uniroot function which looks to solve inverse functions. I am running into a few errors however, and would greatly appreciate help on this.

My goal here is writing a function along the lines of R's base functions qnorm qexp etc. but with qcustom.

# Error 1: (Error in f(x) : argument "p" is missing, with no default)

inverse <- function(f, lower=0.01, upper=500000) {
  function(y) {
    uniroot(function(x) f(x) - y, lower=lower, upper=upper)[1]
  }
}

qcustom <- inverse(function(x, p, a, b) {
  a1 <- p*exp(-a*x)
  a2 <- (1 - p)*exp(-b*x)
  result <- 1 - a1 - a2
  return(result)
})

qcustom(0.5) ##when i add in further parameters, e.g p = 0.5 it says it's an unused parameter##

CodePudding user response：

Let's start at the beginning:

custom_cdf <- function(x, p, a, b) {
   p*exp(-a*x)   (1-p)*exp(-b*x)
}

This has parameters c(p, a, b) and let us try to find a pairing of c(a,b) that makes sense for the range(x) = c(0, 500e3) as you pointed out that you want.

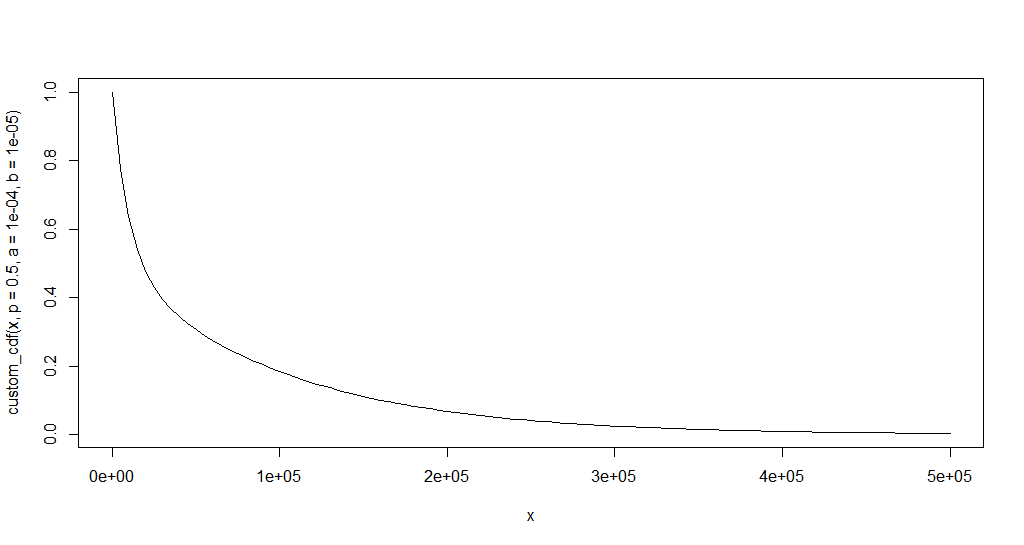
plot.new()
curve(custom_cdf(x, p = 0.5, a = 1e-4, b = 1e-5), xlim = c(0, 500e3))

A reasonable set of values could be:

a <- 1e-4
b <- 1e-5

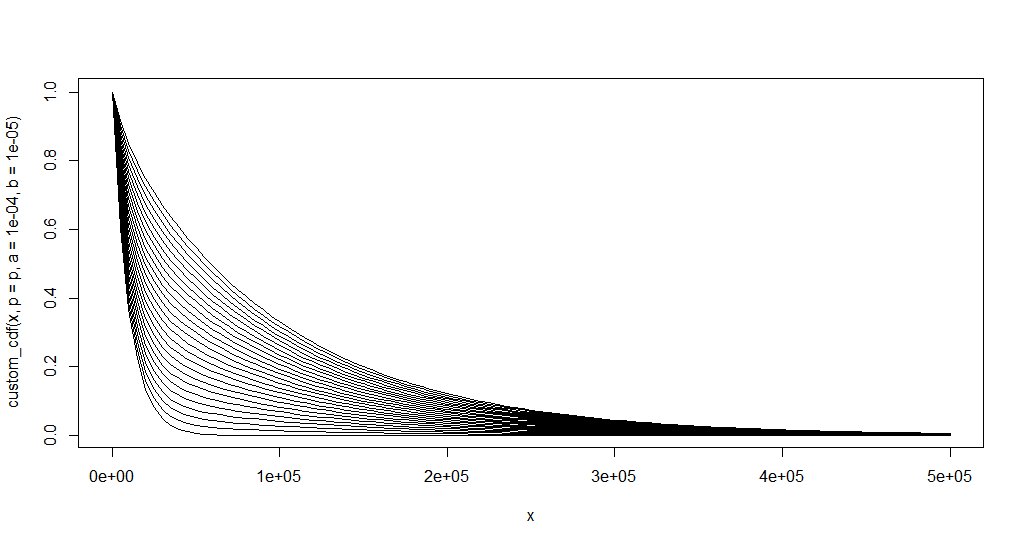
Let us try for multiple values of p:

first <- TRUE
plot.new()
for (p in seq.default(0.1, 1, length.out = 25)) {
  curve(custom_cdf(x, p = p, a = 1e-4, b = 1e-5), xlim = c(0, 500e3), add = !first)
  first <- FALSE
}
rm('p')

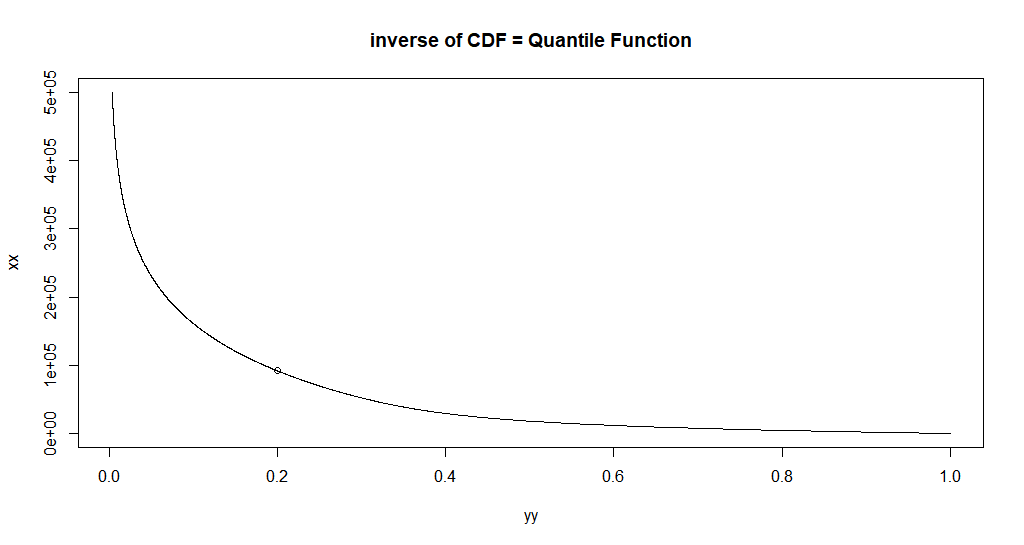
To just the inverse of the CDF, we could just:

xx <- seq.default(0, 500e3, length.out = 2500)
# xx <- seq.default(0, 500e3, by = 10)
# xx <- seq.default(0, 500e3, by = 1)
yy <- custom_cdf(xx, p = 0.5, a = a, b = b)

plot.new()
plot(yy, xx, main = "inverse of CDF = Quantile Function",type = 'l')

I.e. we can just reverse the plotting. So now, this is a picture of the inverse function.

Let's use uniroot to get one inverse value.

uniroot(
  function(x) custom_cdf(x, p = 0.5, a = a, b = b) - 0.2,
  interval = c(0, 100e50),
  extendInt = "yes"
) -> found_20pct_point
#' 
#' Let's plot that point:
#' 
points(custom_cdf(found_20pct_point[[1]], p = 0.5, a = a, b = b), found_20pct_point[[1]])

Alright, so now we understand everything and we can do what you tried to do:

custom_quantile <- function(p, a, b) {
  particular_cdf <- function(x) custom_cdf(x, p, a, b)
  function(prob) {
    uniroot(
      function(x) particular_cdf(x) - prob,
      interval = c(0, 100e50),
      extendInt = "yes"
    )$root
  }
}
custom_quantile_specific <- 
  custom_quantile(p = 0.5, a = a, b = b)
custom_quantile_specific(0.2)

And this works as it yields something close to the desired value.

But regular quantile functions in R does depend on the parameters of the distribution, so this is good enough:

custom_quantile <- function(prob, p, a, b) {
  particular_cdf <- function(x) custom_cdf(x, p, a, b)
  uniroot(
    function(x) particular_cdf(x) - prob,
    interval = c(0, 100e50),
    extendInt = "yes"
  )$root
}
custom_quantile(0.2, p = 0.5, a = a, b = b)