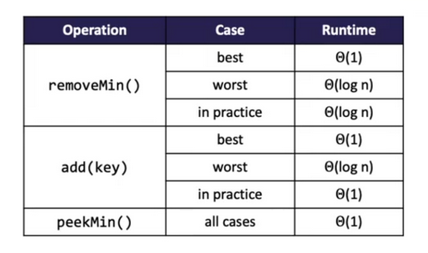
Above is the runtime chart that I got from one of the lecture on Array Implemented Min-Heap.

It says that add is constant in practice with worst time logN.

Would there be a concrete reasoning why in practice, add will be constant run time?

CodePudding user response：

More precisely, the average time complexity of insertion is constant. This applies for repeated insertion or random heaps, basically as long as you're not inserting smaller and smaller values all the time or otherwise making sure that it always has the worst-case complexity.

Very quickly and vaguely explained, the intuition is that basically about half of the nodes of a heap are leaf nodes, and about half of the rest are their parents, etc. So you are very likely to end up at a constant height from the leaf nodes in the tree (which translates to a constant number of updates), and this probability makes up for the rare log(n) scenarios.

If you are interested in formal proofs, this paper should interest you:

Average case analysis of heap building by repeated insertion (accessible here on Waybackmachine).

I also found this Stackoverflow answer for you, which gives some more intuition on the problem.