How to put number of a particular element in a particular row and column constraints in a matrix?-CodePudding

I have to basically create a symmetric matrix of NxN. Which has 1s and 0s randomly populated into it. However the only constraint is I need only one '1' in any row and any column.

I wrote a code to generate the matrix but it has more than one '1' in any row or column. I need to follow the constraint mentioned above, how can i modify my code?

import numpy as np
N = int(input("Enter the number of row and col:"))
my_matrix = np.random.randint(2,size=(N,N))
print(my_matrix)

CodePudding user response：

Create a matrix with zeros. Then, you need to take randomly N row numbers, without repetition, and randomly N column numbers, without repetition. You can use random.sample for this. Then put 1 on the row/column positions.

import numpy as np
from random import sample

N = int(input("Enter the number of row and col:"))
my_matrix = np.zeros((N,N), dtype='int8')
rows = sample(range(N), N)
cols = sample(range(N), N)
points = zip(rows, cols)
for x, y in points:
    my_matrix[x, y] = 1

print(my_matrix)

If you want a symmetrical matrix: In case N is even, I would take N random numbers out of N, half of them as x, half as y; and on both positions (x,y) and (y,x) put a 1. If N is uneven, an additional 1 needs to be put on a random position on the diagonal.

import numpy as np
from random import sample, randint

N = int(input("Enter the number of row and col:"))
even = N%2 == 0

my_matrix = np.zeros((N,N), dtype='int8')
N_range = list(range(N))

if not even:
    diagonal = randint(0, N-1)
    N_range.remove(diagonal)
    my_matrix[diagonal, diagonal] = 1
    N = N - 1

rowcol = sample(N_range, N)

rows = rowcol[:N//2]
cols = rowcol[N//2:]

for x, y in zip(rows,cols):
    my_matrix[x, y] = 1
    my_matrix[y, x] = 1

Here is a better version. Take the first free row, get a random free column, put a 1 on (row,col) and (col,row). Remove the used col/row. Repeat until all numbers 0-(N-1) are used.

import numpy as np
import random

N = int(input("Enter the number of row and col:"))

my_matrix=np.zeros((N,N))
not_used_number = list(range(N))

while len(not_used_number) != 0:
    current_row = not_used_number[0]
    random_col = random.choice(not_used_number)
    my_matrix[current_row, random_col] = 1
    my_matrix[random_col, current_row] = 1
    
    not_used_number.remove(current_row)
    if current_row != random_col:
        not_used_number.remove(random_col)

CodePudding user response：

I did some derivation, and then got a solution with equal probability for each result (However, the performance is barely satisfactory, and it has O(n^2) time complexity).

Derivation process:

Let f(n) be the number of all setting schemes of n * n matrix. Obviously, we have:

f(1) = 1

Then take a convention:

f(0) = 1

For n > 1, I can extract a position from any row and set it to 1. There are two cases:

If 1 is on the diagonal, we can remove the row and column of this 1 and continue to set on the remaining (n - 1) * (n - 1) matrix, so the number of remaining setting schemes is f(n - 1).
If 1 is not on the diagonal, the symmetrical part also needs to be set to 1. Then we can remove the row and column where the two 1's are located. We need to continue to set the remaining (n - 2) * (n - 2) matrix. Therefore, the number of remaining setting schemes is f(n - 2).

Therefore, we can deduce:

f(n) = f(n - 1)   (n - 1) * f(n - 2)

According to the above strategy, if we want to make every setting scheme appear with equal probability, we should give different weights to diagonal index and other indices when selecting index. The weight of the diagonal index should be:

p(n) = f(n - 1) / f(n)

Therefore:

   f(n) = f(n - 1)   (n - 1) * f(n - 2)
     f(n)         (n - 1) * f(n - 2)
=> -------- = 1   ------------------
   f(n - 1)           f(n - 1)
     1
=> ---- = 1   (n - 1) * p(n - 1)
   p(n)
                  1
=> p(n) = ------------------
          (n - 1) * p(n - 1)

The probability function code is as follows:

_prob_cache = [1, 1]


def prob(n):
    """
    Iterative version to prevent stack overflow caused by recursion.
    Old version:
    @lru_cache
    def prob(n):
        if n == 1:
            return 1
        else:
            return 1 / ((n - 1) * prob(n - 1)   1)
    """
    try:
        return _prob_cache[n]
    except IndexError:
        pass

    for i in range(len(_cache) - 1, n):
        _prob_cache.append(1 / (i * _prob_cache[-1]   1))

    return _prob_cache[-1]

Specific implementation:

We use a list to store the indices that can still be used. In each loop, we take the first element of the list as the row index, calculate and build the weight vector, and then wrote a choice function to select the column index from list with reference to the implementation of random.choices, sets the value of the corresponding position, and removes the used index from the list until the list length becomes 1 or 0:

import random

from bisect import bisect
from itertools import accumulate, repeat

import numpy as np


def choice(seq, cum_weights):
    return seq[bisect(cum_weights, random.random())]


def symmetric_permutation(n):
    res = np.zeros((n, n), int)
    remain = list(range(n))

    while True:
        m = len(remain)
        if not m:
            return res
        elif m == 1:
            i = remain.pop()
            res[i, i] = 1
            return res

        primary = prob(m)
        secondary = (1 - primary) / (m - 1)
        i = remain[0]
        j = choice(remain, tuple(accumulate(repeat(secondary, m - 1), initial=primary)))
        res[i, j] = res[j, i] = 1
        remain.remove(i)
        if i != j:
            remain.remove(j)

Here we prepare another function to calculate f(n) for the following test:

def f(n):
    before_prev, prev = 1, 1
    for i in range(1, n):
        before_prev, prev = prev, prev   before_prev * i

    return prev

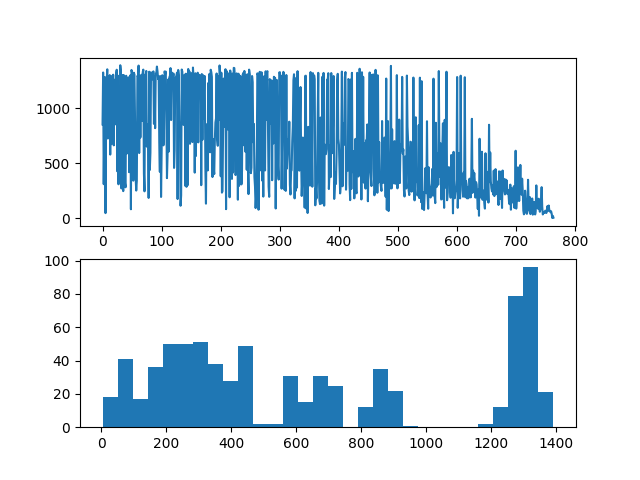
Next is a probability test to verify whether the results are uniform enough. Here I take n=8 and build matries 50_0000 times, use the column index of 1 in each row as the identification of each result, and draw a line graph and histogram of the number of occurrences of each result:

from collections import Counter

import matplotlib.pyplot as plt


random.seed(1)

n = 8
times = 500_000
n_bin = 30

cntr = Counter(tuple(symmetric_permutation(n).nonzero()[1]) for _ in range(times))

assert len(cntr) == f(n)

plt.subplot(2, 1, 1).plot(cntr.values())
plt.subplot(2, 1, 2).hist(cntr.values(), n_bin)
plt.show()

It can be seen from sub figure 1 that the number of occurrences of each result is roughly within the range of 650 ± 70, and it can be observed from sub figure 2 that the distribution of the number of occurrences of each result is close to the Gaussian distribution:

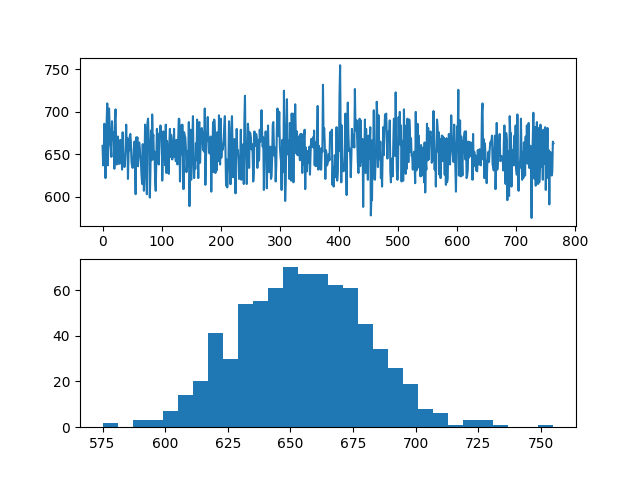
For @AndrzejO 's answer, the same code test is used here, and his solution is faster, but the probability of each result does not seem equal (note that various results also appear here):