Calculate vertical edge coordinates(locations) in splitted & shuffled image-CodePudding

Assume that you have a digital image. You crop that image into 6 pieces vertically. After, you shuffled these pieces and rearrenge these pieces(sub images) randomly. So, you obtain a image like below.

I want to reconstruct the original image like a puzzle. First, we need to calcualte right points on X axis which sub images merged. For example, in the 100th pixel(X-axis), two subsample merged. I have to parse these points to regain sub-images. How can I do that? The image splitted vertically, Is sobel filter on X axis help me to find sharp transition? Any suggestion?

CodePudding user response：

This is an interesting directed graph problem. In each slice the last column has a distance error to the first column. After you build the graph you just need to find the head, and walk along the minimum cost path. I've sketched a script you coult start from start from:

import cv2
import numpy as np
import  matplotlib.pyplot as plt
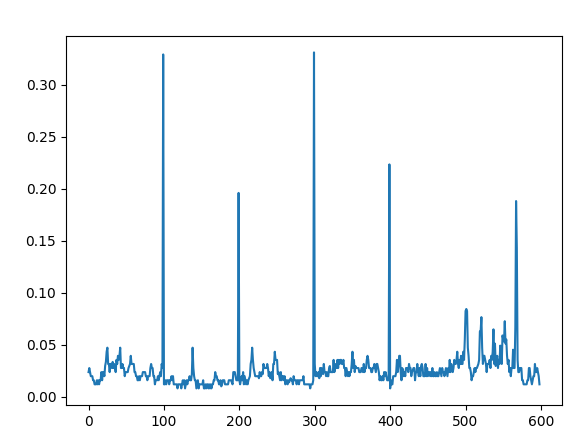
cut_thr = 0.19 # magic number , but kind of arbitrary as if you add a cut, you just make your graph bigger
im = cv2.imread(r'example.png').astype(np.float32)/255 #read image
im = cv2.cvtColor(im,cv2.COLOR_BGR2RGB)
dx=np.abs(np.diff(im,axis=1)) #x difference
dx = np.max(dx,axis=2) #max on all color channels
dx=np.median(dx,axis=0) #max on y axis
plt.plot(dx)

cuts = np.r_[0,np.where(dx>cut_thr)[0] 1,im.shape[1]] #inclusive borders
cuts = [im[:,cuts[i]:cuts[i 1]] for i in range(len(cuts)-1)]
n = len(cuts)
fig,ax = plt.subplots(1,n)
for a,c in zip(ax,cuts):
    a.imshow(c, aspect='auto')
    a.axis('off')

  d = np.ones((n,n))*np.nan # directed connectivity 
    for y in range(n):
        for x in range(y 1,n):
            d[y][x]=np.median(np.abs(cuts[y][:,-1]-cuts[x][:,0]))
            d[x][y]=np.median(np.abs(cuts[x][:,-1]-cuts[y][:,0]))
    src = np.arange(n)
    dst=np.nanargmin(d,axis=1) # the dest of source is the one with the lowest error
    indx=np.where(d==np.nanmin(d))[0][-1] #head, where to begin
    im = cuts[indx]
    for i in range(n-1):
        indx=dst[src[indx]]
        im = np.concatenate([im,cuts[indx]],axis=1)
    plt.figure()
    plt.imshow(im, aspect='equal')