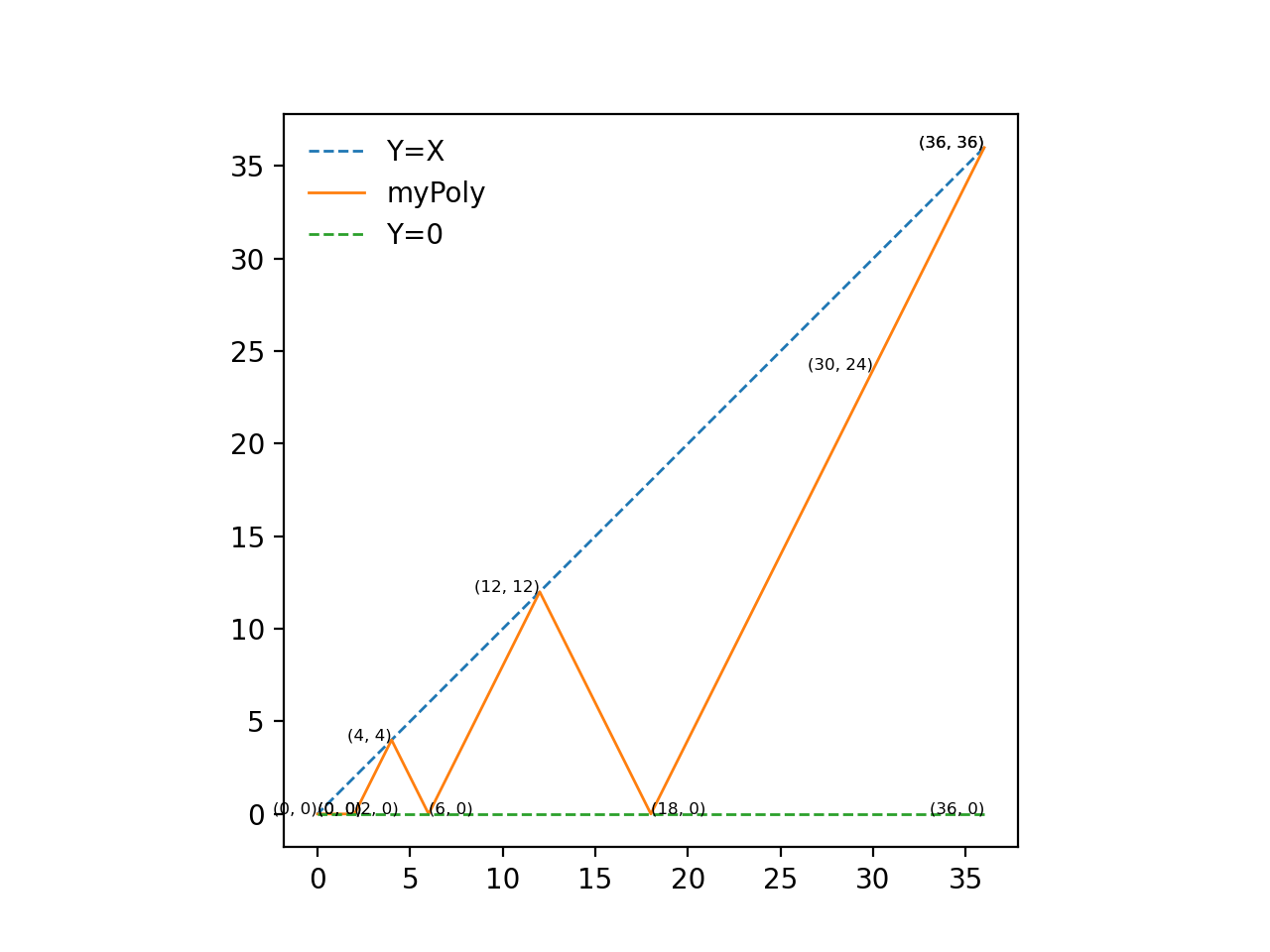
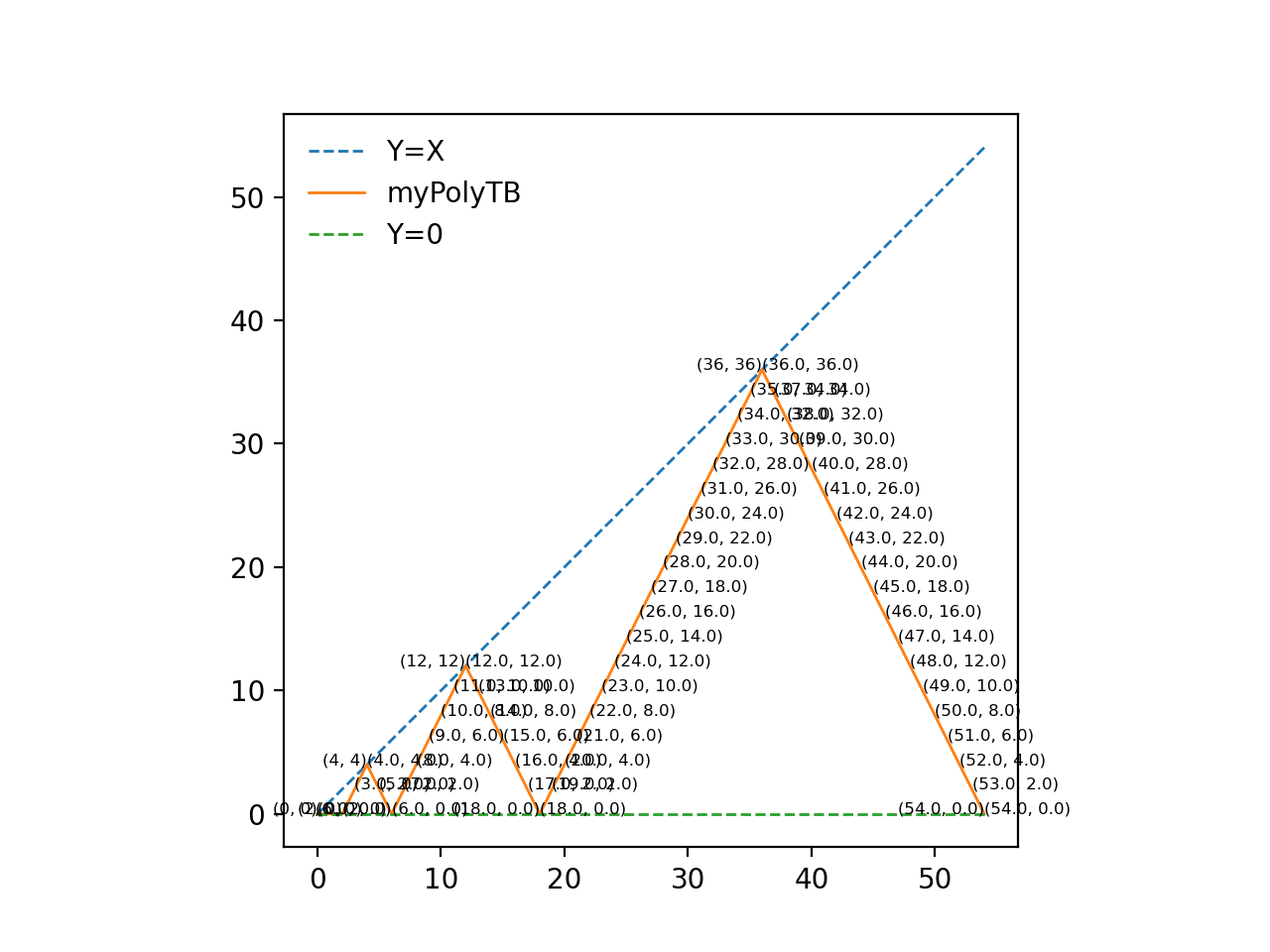
Can I define a line function in one line because it is regular?

graph orenge line : myPoly

Conditions :

The image oscillates between Y=0 and Y=X.

The slope of the line is 2 or -2.

You can start with (2,0).

I want

①Is it possible to define the following part def myPolyY(Ho,myX): in one line?

②Can you do it piecewise or in series?

from sympy import *
var('x y')
import matplotlib.pyplot as plt
def myPolyY(Ho,myX):
    myY=0
    xx=[x[0] for x in Ho]
    yy=[x[1] for x in Ho]
    for i in range(len(xx)-1):
        if xx[i] <= myX & myX<= xx[i 1]:
           myY= (yy[i 1]-yy[i])/(xx[i 1]-xx[i])* (myX - xx[i]) yy[i]
    return myY
def myPolyDef(nMax):
    myPoly=[[0,0],[2,0]]
    i=2
    ans = solve([y - x,
                 y - myPoly[i-1][1] - 2 * (x - myPoly[i-1][0])], [x, y])
    myPoly=myPoly [[ans[x], ans[y]]]
    i=1
    for j in range(nMax):
        i=i 1
        ans=solve([y-0,y-myPoly[i][1] 2*(x-myPoly[i][0])],[x,y])
        myPoly=myPoly [[ans[x],ans[y]]]
        i=i 1
        ans=solve([y-x,
                   y-myPoly[i  ][1]-2*(x-myPoly[i  ][0])], [x,y])
        myPoly=myPoly [[ans[x],ans[y]]]
    return myPoly
def myPolyPlot(Ho,myLabel,myLinestyle):
    plt.plot([x[0] for x in Ho],[x[1] for x in Ho], mec='none', ms=4, lw=1, label=myLabel,linestyle=myLinestyle)
    for i in range(len(Ho)):
        if i % 2==0:
           myPos='right'
        else:
            myPos='left'
        plt.text(Ho[i][0], Ho[i][1], '({x}, {y})'.format(x=Ho[i][0], y=Ho[i][1]),
                  fontsize=6, horizontalalignment=myPos)
    return
def main():
    # myN=4
    myN=2
    myX=30
    myPoly=myPolyDef(myN)
    myY=myPolyY(myPoly,30)
    # matplotlib
    myH=max(list(map(lambda x: max(x), myPoly)))
    plt.axes().set_aspect('equal')
    plt.text(myX,myY, '({x}, {y})'.format(x=myX, y=myY),
             fontsize=6, horizontalalignment='right')
    myPolyPlot([[myH,myH],[0,0]],'Y=X','--')
    myPolyPlot(myPoly,'myPoly','-')
    myPolyPlot([[myH,  0],[0,0]],'Y=0','--')
    plt.legend(frameon=False, fontsize=10, numpoints=1, loc='upper left')
    plt.savefig('myPoly.png', dpi=200)
    plt.show()
if __name__ == '__main__':
    main()

(2022-03-03)　I used log.

from sympy import *
import matplotlib.pyplot as plt
var('x y')
def myCal_PolyTopBottom(myT):
    myPolyTB = [[0, 0], [2, 0]]
    for x in range(myT):
        xt = 4*(3**x)
        yt = 4*pow(3, int(log(xt // 2, 3)))
        myPolyTB = myPolyTB   [[xt           , yt ]]
        myPolyTB = myPolyTB   [[xt   yt * 0.5, 0.0]]
    return myPolyTB
def myCal_PolyXYN(myPolyTB,myXmax):
    myPolyXYN = [[0, 0], [2, 0]]
    for x in range(3, int(myXmax) 1):
        y=myCal_PolyXYi(myPolyTB,x)
        myPolyXYN = myPolyXYN   [[float(x), y]]
    return myPolyXYN
def myCal_PolyXYi(Ho,myX):
    xx=[x[0] for x in Ho]
    yy=[x[1] for x in Ho]
    for i in range(len(xx)-1):
        if xx[i] <= myX & myX<= xx[i 1]:
           myY= (yy[i 1]-yy[i])/(xx[i 1]-xx[i])* (myX - xx[i]) yy[i]
    return myY
def myPlot_Poly(Ho,myLabel,myLinestyle):
    plt.plot([x[0] for x in Ho],[x[1] for x in Ho],
             mec='none', ms=4, lw=1, label=myLabel,linestyle=myLinestyle)
    return
def myPlot_Text(Ho,myPos):
    for i in range(len(Ho)):
        plt.text(Ho[i][0], Ho[i][1], '({x}, {y})'.format(x=Ho[i][0], y=Ho[i][1]),
                  fontsize=6, horizontalalignment=myPos)
    return
def main():
    myT=3
    myPolyTB=myCal_PolyTopBottom(myT)
    myH=max(list(map(lambda x: max(x),myPolyTB)))
    myPolyN=myCal_PolyXYN(myPolyTB,myH)
# matplotlib
    plt.axes().set_aspect('equal')
    myPlot_Text(myPolyTB,'right' )
    myPlot_Text(myPolyN ,'left'  )
    myPlot_Poly([[myH,myH],[0,0]],'Y=X'     ,'--')
    myPlot_Poly(  myPolyTB       ,'myPolyTB','-' )
    myPlot_Poly([[myH,  0],[0,0]],'Y=0'     ,'--')
    plt.legend (frameon=False, fontsize=10, numpoints=1, loc='upper left')
    # plt.savefig('myPoly.png', dpi=200)
    plt.show()
if __name__ == '__main__':
    main()

CodePudding user response：

If you look at the first triangle, it is easy to see that the equation can be expressed as

y = 4 - 2 * abs(4-x)

More generally, each triangle has a top value, and the corresponding equation is

y = top - 2 * abs(top-x)

Then, for each coordinate x, we have to determine the value of the corresponding top

top = 4 * pow(3, int(log(x//2,3)))

from math import *

myPoly=[[0,0],[2,0]]
for x in range(3, 37):
    val = 4 * pow(3, int(log(x//2,3)))
    y = val - 2 * abs(x - val)
    myPoly = myPoly [[x,y]]