In a project, I'd like to evenly distibute dots around a regular hexagon path.
Thus I'd like to calculate the coordinates of my dots from the center of the hex and the length of a side.

For instance, if I want to do the same thing around a circle I would do (in JS) :

let center = {x: 0, y: 0}
let radius = 10;
let amountOfDots = 48;
for (let i = 0; i < amountOfDots; i  ) {
    let x = radius * Math.sin(Math.PI * 2 * i / amountOfDots)   center.x;
    let y = radius * Math.cos(Math.PI * 2 * i / amountOfDots)   center.y;
    // draw my dot in (x, y) or whatever
}

In other words, I would like to get the coordinate of all those points in a single loop.
On this Exemple amountOfDots = 24

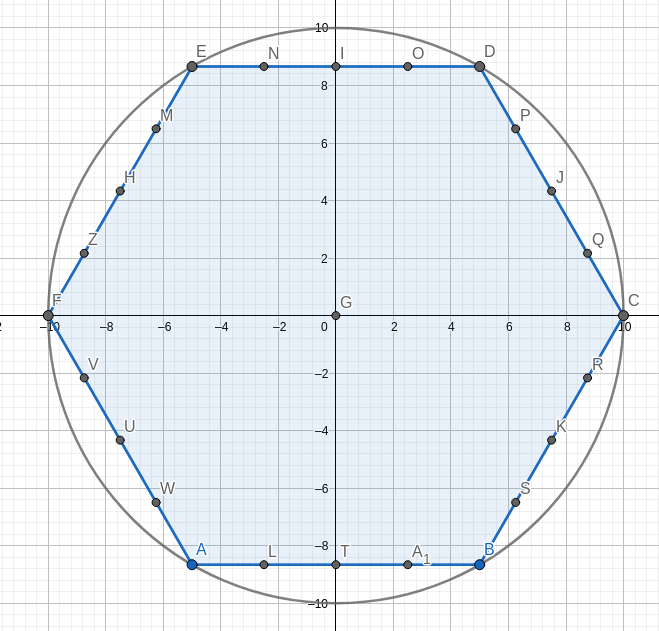
I have the intuition it wouldn't be too hard to implement, but I'm struggling with the maths...
Thanks :)

CodePudding user response：

A few observations when we do this on the unit circle (radius = 1):

• The size of one of the six hexagon edges is 1

• The coordinates of the six points of the hexagon are:

  ( 1,    0   )  
  ( 0.5,  √3/2)
  (-0.5,  √3/2)
  (-1,    0   )
  (-0.5, -√3/2)
  ( 0.5, -√3/2)
  

• The total size of the hexagon's circumsphere is 6.

• The distance (on that circumsphere) between two consecutive dots is 6 / amountOfDots

• The distance of a dot to the starting point (on the hexagon) can be used to know on which hexagon edge this point lies (the integer part of the distance), and how far on that edge (the fractional part of the distance)

• Using interpolation we can thus determine the coordinates of such a dot

Here is an interactive JS snippet to calculate and draw those points:

// Main algorithm:
function hexagonDots(center, radius, amountOfDots) {
    // Function to map unit coordinates to the given center & radius
    const project = (x, y) => ({
        x: center.x   radius * x,
        y: center.y   radius * y
    });
    const y = Math.sqrt(3) / 2; // = sin(60°)
    const hexaX = [1, 0.5, -0.5, -1, -0.5, 0.5, 1];
    const hexaY = [0, y, y, 0, -y, -y, 0];

    return Array.from({length: amountOfDots}, (_, i) => {
        let offset = 6 * i / amountOfDots;
        const edgenum = Math.floor(offset); // On which edge is this dot?
        offset %= 1; // Retain fractional part only: offset on that edge
        return project( 
            // Use interpolation to get coordinates of that point on that edge
            hexaX[edgenum]   offset * (hexaX[edgenum   1] - hexaX[edgenum]),
            hexaY[edgenum]   offset * (hexaY[edgenum   1] - hexaY[edgenum])
        );
    });
}

// I/O management:

function drawHexagon(ctx, dots) {
    // Draw
    ctx.resetTransform();
    ctx.clearRect(0, 0, ctx.canvas.width, ctx.canvas.height); 
    ctx.translate(200, 80);
    for (const {x, y} of dots) {
        ctx.beginPath();
        ctx.moveTo(x, y);
        ctx.lineTo(x 1, y);
        ctx.stroke();
    }
}

const ctx = document.querySelector("canvas").getContext("2d");

function refresh() {
    const center = {x: 0, y: 0};
    const radius = 70;
    const amountOfDots =  this.value;
    const dots = hexagonDots(center, radius, amountOfDots);
    drawHexagon(ctx, dots);
}

const input = document.querySelector("input");
input.addEventListener("input", refresh);
refresh.call(input);

Dots: <input type="number" value="48" size="4"><br>
<canvas></canvas>