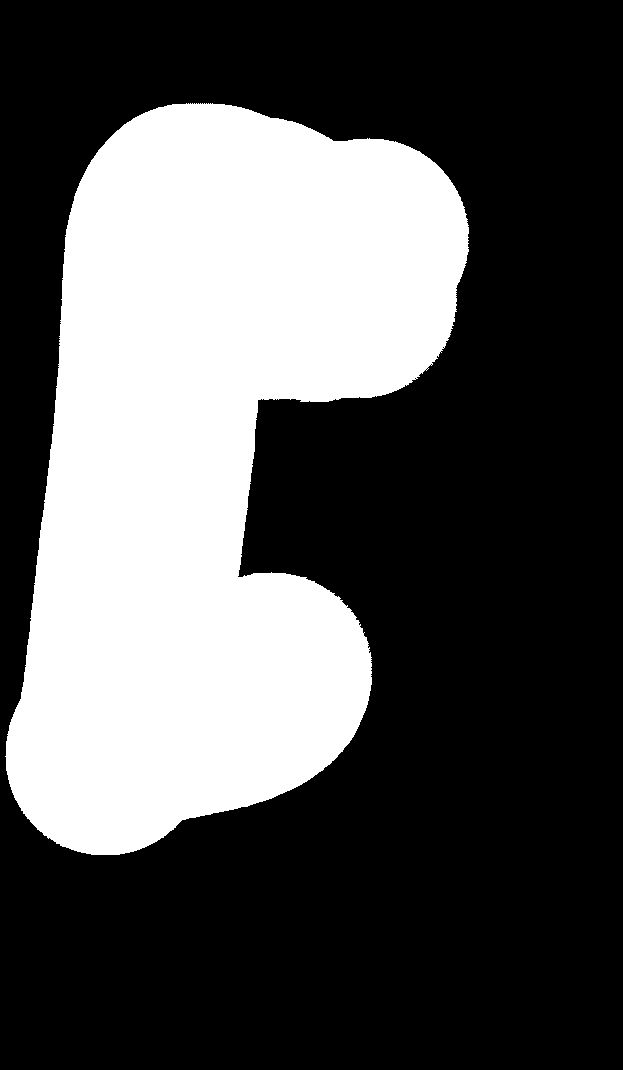numpy - find all pixels near a set of pixels-CodePudding

I have a PIL.Image object input of mode '1' (a black & white bitmap) and I would like to determine, for every pixel in the image, whether it's within n pixels (Euclidean distance - n may be around 100 or so) of any of the white pixels.

The motivation is: input represents every pixel that is different between two other images, and I would like to create a highlight region around all those differences to show clearly where the differences occur.

So far I haven't been able to find a fast algorithm for this - the following code works, but the convolution is very slow because the kernel argument is larger than the convolution can apparently handle efficiently:

from scipy import ndimage
import numpy as np
from PIL import Image

n = 100
y, x = np.ogrid[:2*n, :2*n]
kernel = (x-n)**2   (y-n)**2 <= n**2

img = Image.open('input.png')
result = ndimage.convolve(np.array(img), kernel) != 0
Image.fromarray(result).save('result.png')

Example input input.png:

Desired output result.png (there are also some undesired artifacts here that I assume come from over/underflow):

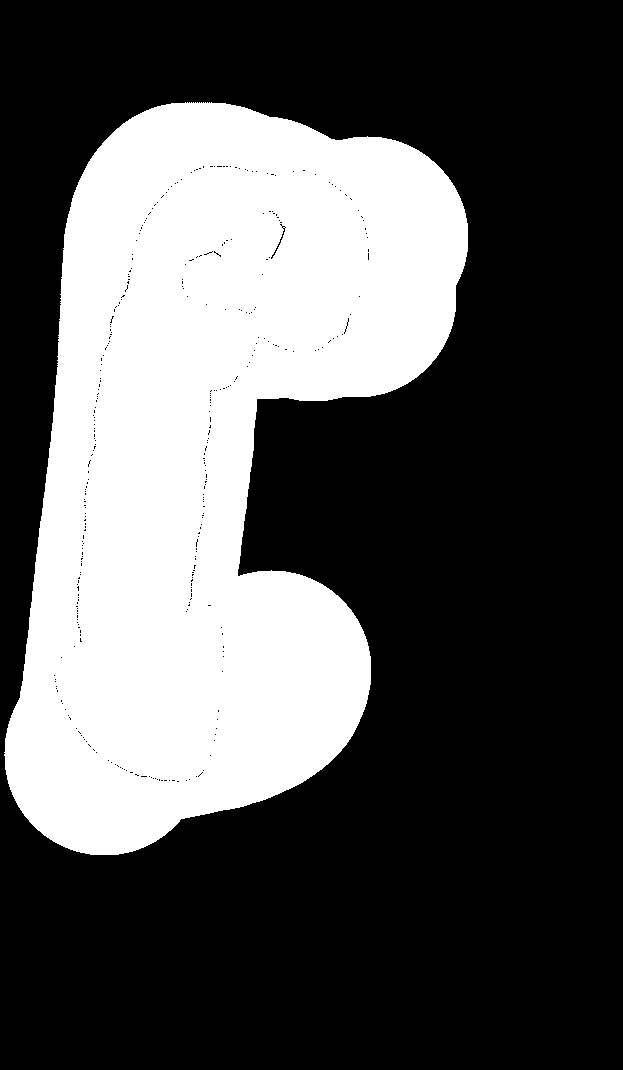
Even with these small images, the computation takes 30 seconds or so. Can someone recommend a better procedure to compute this? Thanks.

CodePudding user response：

ndimage.convolve use a very inefficient algorithm to perform the convolution certainly running in O(n m kn km) where (n,m) is the shape of the image and (kn, km) is the shape of the kernel. You can use an FFT to do that much more efficiently in O(n m log(n m)) time. Hopefully, scipy provide such a function. Here is an example of usage:

import scipy.signal
import numpy as np
from PIL import Image

n = 100
y, x = np.ogrid[:2*n, :2*n]
kernel = (x-n)**2   (y-n)**2 <= n**2

img = Image.open('input.png')
result = scipy.signal.fftconvolve(img, kernel, mode='same') >= 1.0
Image.fromarray(result).save('result.png')

This is >500 times faster on my machine and this also fix the artefacts. Here is the result: