Creating and plotting confidence intervals-CodePudding

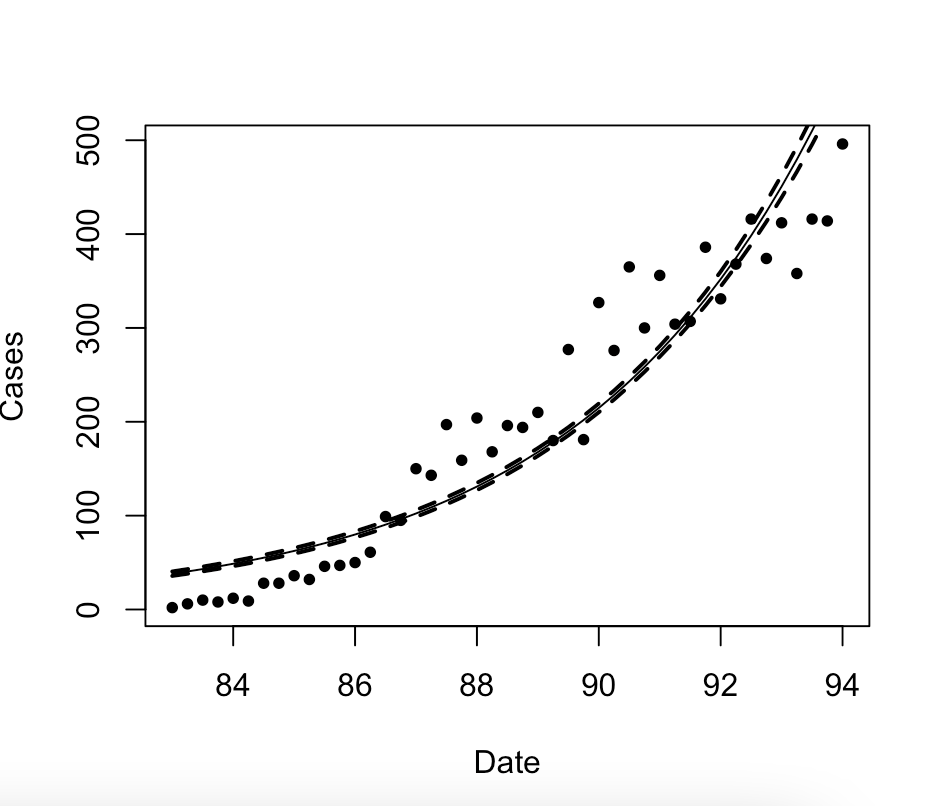
I have fitted a gaussian GLM model to my data, i now wish to create 95% CIs and fit them to my data. Im having a couple of issues with this when plotting as i cant get them to capture my data, they just seem to plot the same line as the model without captuing the data points. Also Im also unsure that I've created my CIs the correct way here for the mean. I entered my data and code below if anyone knows how to fix this

data used

aids
 cases quarter  date
1      2       1 83.00
2      6       2 83.25
3     10       3 83.50
4      8       4 83.75
5     12       1 84.00
6      9       2 84.25
7     28       3 84.50
8     28       4 84.75
9     36       1 85.00
10    32       2 85.25
11    46       3 85.50
12    47       4 85.75
13    50       1 86.00
14    61       2 86.25
15    99       3 86.50
16    95       4 86.75
17   150       1 87.00
18   143       2 87.25
19   197       3 87.50
20   159       4 87.75
21   204       1 88.00
22   168       2 88.25
23   196       3 88.50
24   194       4 88.75
25   210       1 89.00
26   180       2 89.25
27   277       3 89.50
28   181       4 89.75
29   327       1 90.00
30   276       2 90.25
31   365       3 90.50
32   300       4 90.75
33   356       1 91.00
34   304       2 91.25
35   307       3 91.50
36   386       4 91.75
37   331       1 92.00
38   368       2 92.25
39   416       3 92.50
40   374       4 92.75
41   412       1 93.00
42   358       2 93.25
43   416       3 93.50
44   414       4 93.75
45   496       1 94.00

my code used to create the model and intervals before plotting

#creating the model
model3 = glm(cases ~ date,
         data = aids,
         family = poisson(link='log'))

#now to add approx. 95% confidence envelope around this line
#predict again but at the linear predictor level along with standard errors
my_preds <- predict(model3, newdata=data.frame(aids), se.fit=T, type="link") 

#calculate CI limit since linear predictor is approx. Gaussian
upper <- my_preds$fit 1.96*my_preds$se.fit #this might be logit not log
lower <- my_preds$fit-1.96*my_preds$se.fit

#transform the CI limit to get one at the level of the mean
upper <- exp(upper)/(1 exp(upper)) 
lower <- exp(lower)/(1 exp(lower))

#plotting data
plot(aids$date, aids$cases,
 xlab = 'Date', ylab = 'Cases', pch = 20)

#adding CI lines
plot(aids$date, exp(my_preds$fit), type = "link",
 xlab = 'Date', ylab = 'Cases') #add title
lines(aids$date,exp(my_preds$fit 1.96*my_preds$se.fit),lwd=2,lty=2)
lines(aids$date,exp(my_preds$fit-1.96*my_preds$se.fit),lwd=2,lty=2)

outcome i currently get with no data points, the model is correct here but the CI isnt as i have no data points, so the CIs are made incorrectly i think somewhere

CodePudding user response：

Edit: Response to OP's providing full data set.

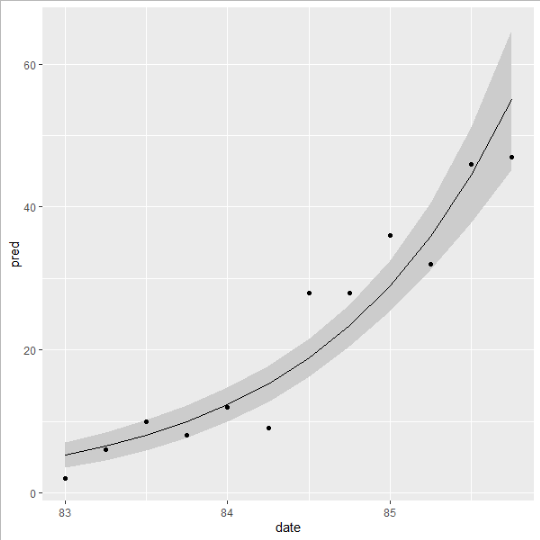
This started out as a question about plotting data and models on the same graph, but has morphed considerably. You seem you have an answer to the original question. Below is one way to address the rest.

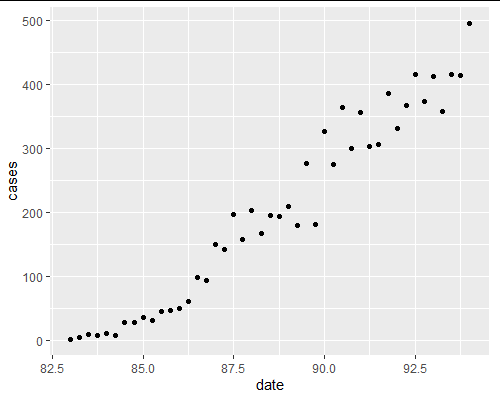
Looking at your (and my) plots it seems clear that poisson glm is just not a good model. To say it differently, the number of cases may vary with date, but is also influenced by other things not in your model (external regressors).

Plotting just your data suggests strongly that you have at least two and perhaps more regimes: time frames where the growth in cases follows different models.

ggplot(aids, aes(x=date))   geom_point(aes(y=cases))

This suggests

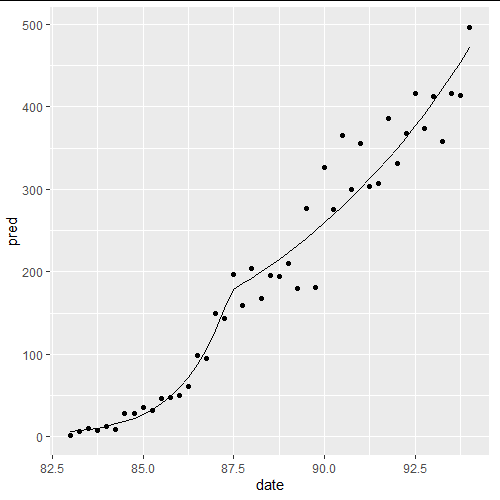
Note that we need to tell segmented the count of breakpoints, but not where they are - the algorithm figures that out for you. So here, we see a regime prior to 3Q87 which is well modeled using poission glm, and a regime after that which is not. This is a fancy way of saying that "something happened" around 3Q87 which changed the course of the disease (at least in this data).

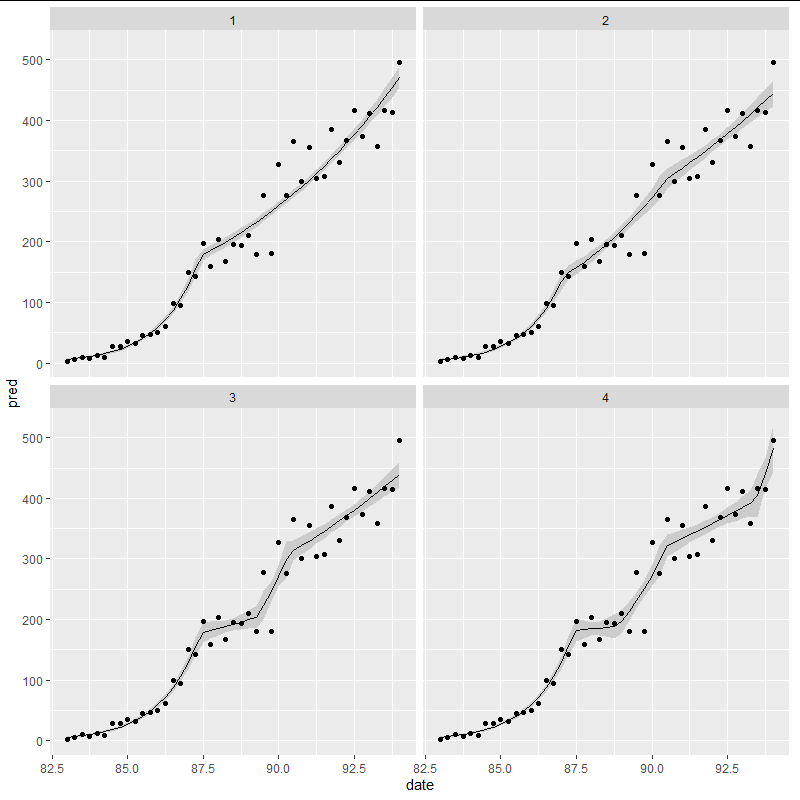
The code below does the same thing but for between 1 and 4 breakpoints.

get.pred <- \(p.n, p.DT) {
  fit     <- glm(cases~date, p.DT, family=poisson)
  seg.fit <- segmented(fit, seg.Z = ~date, npsi=p.n)
  predict(seg.fit, type='response', se.fit=TRUE)[c('fit', 'se.fit')]
}
gg.dt <- rbindlist(lapply(1:4, \(x) { copy(aids)[, c('pred', 'se'):=get.pred(x, .SD)][, npsi:=x] } ))
ggplot(gg.dt, aes(x=date)) 
  geom_ribbon(aes(ymin=pred-1.96*se, ymax=pred 1.96*se), fill='grey80') 
  geom_line(aes(y=pred)) 
  geom_point(aes(y=cases)) 
  facet_wrap(~npsi)

Note that the location of the first breakpoint does not seem to change, and also that, notwithstanding the use of the poisson glm the growth appears linear in all but the first regime.

There are goodness-of-fit metrics described in the package documentation which can help you decide how many break points are most consistent with your data.

Finally, there is also the

Or, you could let ggplot do all the work for you.

ggplot(aids, aes(x=date, y=cases)) 
  stat_smooth(method = glm, method.args=list(family=poisson)) 
  geom_point()