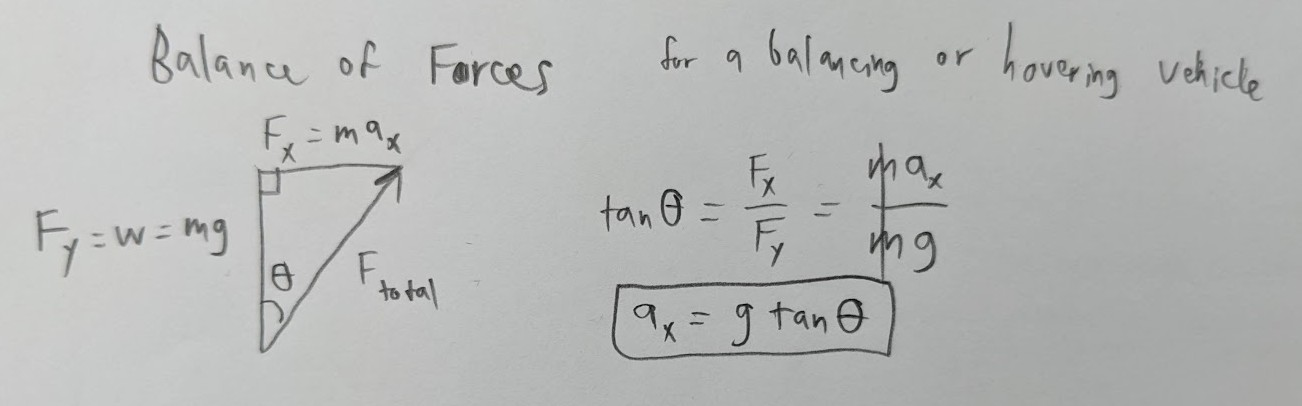I'm trying to design a controller to balance a 2-wheels robot (around 13kg) and making it robust against external forces (e.g. if someone kicks it, it should not fall and not drift indefinitely forward/backward). I'm pretty experienced with most control techniques (LQR, Sliding Mode Control, PID etc), but I've seen online that most people use LQR for balancing 2-wheels robots, hence I'm going with LQR. My problem is that, despite I'm able to make the robot not fall down, it rapidly starts going forward/backward indefinitely, and I don't how to make it mantain a certain position on the ground. What I want to achieve is that, when the robot gets kicked by an external force, it must be able to stop moving forward/backward while mantaining the balance (it's not necessary to mantain a position on the ground, I just want the robot to stop moving). The measurements to which I have access from the sensors are: position on both wheels (x), velocity of both wheels (x_dot), angular position of robot (theta), angular velocity of robot (theta_dot). Since now I tried 2 approaches:

1. set all reference signals to 0 and try to tune the LQR gain. With this (simple) approach I'm not sure if the coefficients of gain K relative to x and theta should have same or opposite sign, because, if for example the robot gets kicked away from its reference for x, the wheels should move in the direction that makes the robot return to the 0 point, but this would make theta go in the opposite direction. When the robot gets kicked, I would like that first theta gets adjusted in order to brake the movement given by the external force, and then x_dot should go in the same direction as theta in order to stop the robot.
2. use best LQR gains that I could find empirically/with MATLAB and use some "heuristic" in order to, given the current state of the robot (x, x_dot, theta, theta_dot), choose the reference signals for the state variables. I tried the heuristic "if x_dot goes forward/backward, then make theta inclide backward/forward", which makes the robot avoid drifting forward/backward in case there're no disturbances, but if I kick the robot it starts oscillating really fast until it falls (I tried to adjust the K gain of LQR to solve this problem, but I couldn't find any that solved it).

Which approach would you suggest me to use? Should I implement some more sophisticated heuristics (any suggestion?) or should I just tune the LQR gain until I find the perfect one? Should I consider using an integrator (for controlling which states?) together with the LQR?

Any advice would be highly appreciated. I'm kind of desperate.

CodePudding user response：

The type of sensory system, the computation unit on board etc. would definitely define the approach you are taking. Since you did not give more details regarding the setup, let us assume you have a IMU aligned with the body frame and you have a method of computing roll, pitch and yaw of the robot at a given moment. Also let the speed at which u can compute RPY, is at least twice the speed of the main system loop.

You may want to start by designing three independent PID controllers, each for the three axis with 0 degrees being the target state that you want to maintain. Quite a while back, I was able to make my quadrotor self-balance by constraining two axes and tuning one at a time. In your case, you would first make the PID responsible for one of the axis be able to bring the robot to neutral position for a range of external disturbance that you expect the system to face during operation. A PID won't be able to respond fast enough if you had say tuned for say 5 - 10 N force kicks but later subjected to 100 N kick.

Give this a try and maybe furnish the question with details regarding the robot, the type of wheels u are using and so forth.

Good luck.

CodePudding user response：

Physics-based controls, and control systems: the many layers of control

AKA: a full description of all of the necessary control loops for a robust vehicle controller, including for self-balancing systems like 2-wheeled self-balancing Segway-like robots, or quadcopters/drones.

In any complicated control system, you have to have multiple layers of controllers.

From inner-most to outer-most controller, here is what you need:

1. Pitch angle controller: In your case, your inner-most controller sounds like it is pitch angle: I think you are using an LQR controller to adjust wheel motor throttle to control pitch angle. You could also use a PID controller for this.

   If you make your pitch angle set-point 0 deg, then the robot will stay stationary standing straight up so long as no outside force acts upon it, and so long as it also began at rest. If you push the robot, it will start to translate linearly (ex: move forward or backwards), at the constant velocity you imparted upon it, while maintaining a fixed, upright angle. Essentially, keeping your pitch angle set-point at 0 degrees makes this the same as giving a shove to a motorless ball or cart--it will keep rolling in the direction you push it per Newton's 1st Law of Motion, which is about inertia: an object in motion stays in motion.

2. Linear acceleration controller: You need to add an outer controller where you adjust pitch angle to control linear acceleration (forwards or backwards).

   Think about it like this: this is a physics problem: the more a 2-wheeled Segway-like robot is tilted forward, the faster gravity causes it to "fall forward". The faster it "falls forward", the faster you must drive those wheels to try to get those wheels back underneath it, to make it maintain a fixed tilt angle rather than continuing to tilt further until it hits the ground. Moving the wheels underneath it to prevent it from falling over causes it to accelerate in that direction.

   For a tilted vehicle at a fixed altitude (for air vehicles; or on a level surface, for ground vehicles) and at a fixed tilt angle, the linear acceleration, a, is: a = g*tan(theta), where g = acceleration due to gravity = 9.81 m/s^2, and theta = tilt angle. Here is a "Balance of Forces" diagram (side view: down is towards the ground and up is towards the sky) I just drew:

   

   Solve for theta (tilt angle), and you get: theta = atan(a/g).

   So, a in a translational (forwards or backwards) direction is in units of m/s^2. Over time (s), this translational acceleration results in a certain translational velocity (m/s^2 * s = m/s). So, if you hold it tiled for a moment, let it accelerate, and then stand it back up straight again, you'll now be continuing forward at a fixed velocity, assuming level ground and no friction. That's what's happening to you when someone pushes or kicks it! To counter this translational velocity, you'll need a velocity controller which applies the necessary acceleration in the opposite direction in order to stop the vehicle's motion.

3. Linear velocity controller: The next controller is a velocity controller. You need to set a desired velocity (ex: 0 m/s to stop the vehicle). In this controller, you adjust linear acceleration to control linear velocity.

   You can then set a tuning parameter, tau [sec], which is the time constant over which period you'd like to achieve your desired velocity. Tune this to be very small for a fast response, and for systems with low inertia, and tune it to be very large for a slow response, and for systems with high inertia. If you tune it too low, the system will have bad jitter and respond to noise--kind of like setting your control loop too fast. If you tune tau too high, the system will be very slow and sluggish to respond. Essentially, tau is like a "gain" tuning parameter.

   This is another layer with a physics-based controller. You need the physics equation of motion for this: dv [m/s] = a * dt [sec]. Solve for a and you get a = dv/dt. So, if your actual velocity is 2.5 m/s and your desired velocity is 0 m/s, then the desired velocity change, dv, that you need is 2.5 m/s - 0 m/s = 2.5 m/s. The time period, tau, over which you'd like to accomplish this is your dt (time change, in sec), in this case. So, if tau = 2 sec, then the necessary acceleration you need to achieve this velocity change over that time period tau is a = dv/dt = 2.5m/s / 2 sec = 1.25 m/s^2.

   This liner acceleration required by your linear velocity controller here is your input to the linear acceleration controller above. Solve for pitch angle, theta, from the linear acceleration controller above: theta = atan(a/g) = atan(1.25 m/s^2 / 9.81 m/s^2) = atan(0.12742) = 0.1267 rad x 180 deg/pi rad = 7.26 deg. So, input 7.25 deg (with the correct sign, per your situation) as your set-point into your pitch angle controller in order to begin decelerating from 2.5 m/s to 0 m/s over a timer period, tau, of 2 sec.

   Run the inner control loop as fast as is reasonable, perhaps 50 to 500 Hz.

   Run the outer control loops as fast as is reasonable, perhaps 25 to 50 Hz.

   The farther "outside" that your control loop is, the slower you can run your control loop. Self-driving cars, for instance, run their outer-most control loops at around 10 Hz, partly since this is good enough, and partly since the computational complexity is so high that this is all the computers can do.

   So, your linear velocity controller calculates a desired acceleration which feeds into your linear acceleration controller, which calculates a desired tilt angle, or pitch, which feeds into your pitch angle controller, which adjusts motor throttles to achieve that pitch.

   To achieve your objective you stated, of no longer rolling forwards, you'd stop there.

But, I'd go further:

4. Linear position controller: You will adjust linear velocity over time to control linear position. With your wheel encoders, you can figure out how far you've gone, and control position to get the robot to return back to where it started. Or, you can simply command any arbitrary position to have it drive certain distances and navigate around the room.

   Essentially, you'd simply command some non-zero velocity in a direction you want, and numerically integrate that over time to get distance. Use trapezoidal integration, as I explain here: Numerical derivation and integration in code for physics, mapping, robotics, gaming, dead-reckoning, and controls. The simple idea is that velocity [m/s] x time [s] = distance [m].

Remember that for all these controllers, you read the wheel encoders to determine wheel motion.

The types of controllers you will be using in your case are these, again, from inner-most to outer-most controller:

1. Pitch angle controller: LQR (from what you said). You could also use PID.
2. Linear acceleration controller: A physics-based feed-forward (the bulk of the control input).
   1. Optionally, add a PID feedback on the error of actual vs commanded linear acceleration to tune it so that the actual linear acceleration approaches the commanded linear acceleration.
   2. Sum the outputs from the feed-forward physics-based controller and from the PID feedback controller.
3. Linear velocity controller: A physics-based feed-forward (the bulk of the control input for low speeds).
   1. Optionally, add another layer of physics control to compensate for air resistance as velocity increases. Drag [N] = C_D*q*A, where C_D [unitless] is your experimental drag coefficient for your particular vehicle's shape properties and how that shape interacts with the fluid of interest (air in our case), q [N/m^2] = dynamic pressure = 1/2 * rho * v^2, where rho [kg/m^3] is air density, and v [m/s] is velocity, and A [m^2] is frontal area (which is geometry-based, since it decreases the more the robot is tilted). THEN, on top of that extra physics-based layer which accounts for air resistance as the robot speeds up:
   2. Optionally, add a PID feedback on error of actual vs commanded linear velocity to tune it so that the actual linear velocity approaches the commanded linear velocity.
   3. Sum the outputs of all controllers.
4. Linear position controller: A simple "physics-based" (integration of velocity with respect to time) feed-forward controller to achieve a desired trajectory over time, OR:
   1. A PID controller on actual vs desired position (keep a total /- wheel encoder displacement count, and seek to zero it--the larger the position or distance "error", the stronger the commanded linear velocity towards the target point should be).
   2. The above linear position controllers are both "dead-reckoning"-based. To add any feedback controllers on top of this would require a position "truth source", such as camera-based positioning systems, acoustic-based positioning systems, GPS, etc., to tweak your position estimates slowly over time.

Anyway, the way I see it, that's the idea. That's the type of approach I took on my quadcopter controller: Quadrotor 2 - Physics-based Flight controller demo w/lead point navigation & Arduino interface to RC Tx, and that controller would also work perfectly for a 2-wheeled Segway-like self-balancing robot, too, since the quadcopter is governed by the same principles as the self-balancing robot. Controls has many options and layers. Physics should be part of many if not most of them.

I'll also mention that I believe the entire thing above could be done on almost any computational platform, from a single Arduino Nano (ATmega328 microcontroller), to a powerful desktop Linux laptop. It just requires the right amount of software skill is all, I think. Engineering is hard. Programming is complicated.

Lastly, please leave some comments under this question with some resources to teach me LQR controllers. I don't know how to write one. I've used PID and physics is all.

References:

1. My answer: Numerical derivation and integration in code for physics, mapping, robotics, gaming, dead-reckoning, and controls
2. My physics notes from college: eRCaGuy_Engineering/Equation_Sheets/Physics 110 (General Physics I) - Constants and Equations - Staples#2.pdf
3. My quadcopter simulation: 1/3 - Autonomous quadcopter guidance and control (physics-based pure pursuit simulation)
   1. See the notes under this video. I jotted down there that a = F/m = g*tan(tilt_angle). That's how I was able to remember how to draw my "Balance of Forces" diagram above.
4. My quadcopter live demo of my physics-based controller I described above: 3/3 - Autonomous quadcopter guidance & control (physics-based pure pursuit demonstration)
5. All 3 of my flight controller videos: https://github.com/ElectricRCAircraftGuy#flight-controller-videos
6. https://en.wikipedia.org/wiki/Equations_of_motion