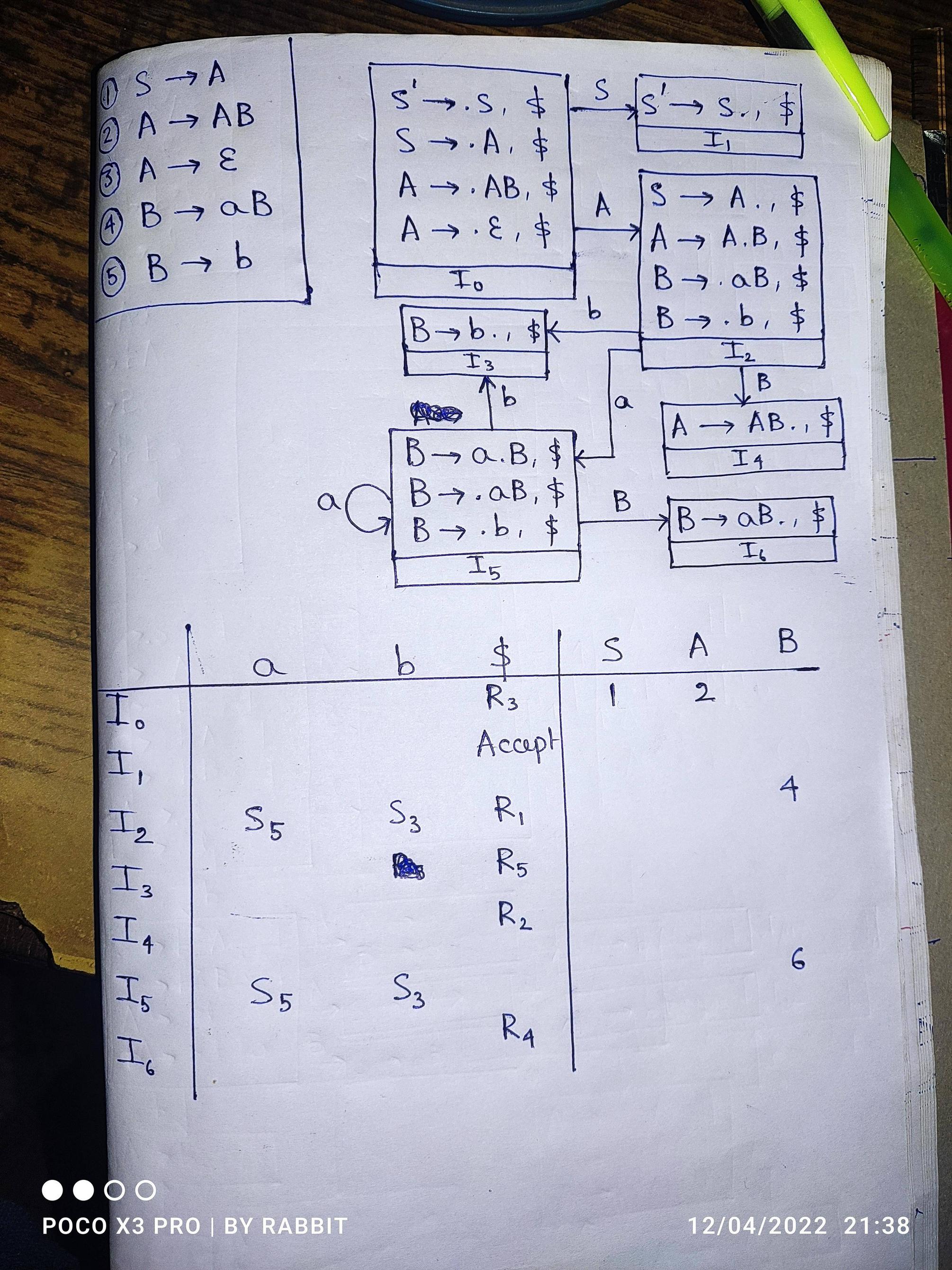
Given the following grammar:

1. S -> A
2. A -> AB
3. A -> ϵ
4. B -> aB
5. B -> b

Check whether it is CLR(1) or not.

I have drawn the canonical itemsets as well as the parse table. But I'm not sure whether it is actually correct or not. I have tried searching for some similar examples that have epsilon productions but could not find any. Could someone please help me out?

CodePudding user response：

The initial state of your parser is I0, and $ is the only lookahead-terminal for which I0 has an action. So if the input is anything other than the empty string, your parser will raise an error. But the grammar has non-empty strings in its language. So this can't be a correct parser for the grammar.

I think your main mistake is in propagating lookaheads. For example, when you close A -> .AB, $, you need to add A -> .whatever items with lookaheads equal to each terminal in FIRST(B$), and you haven't done that.