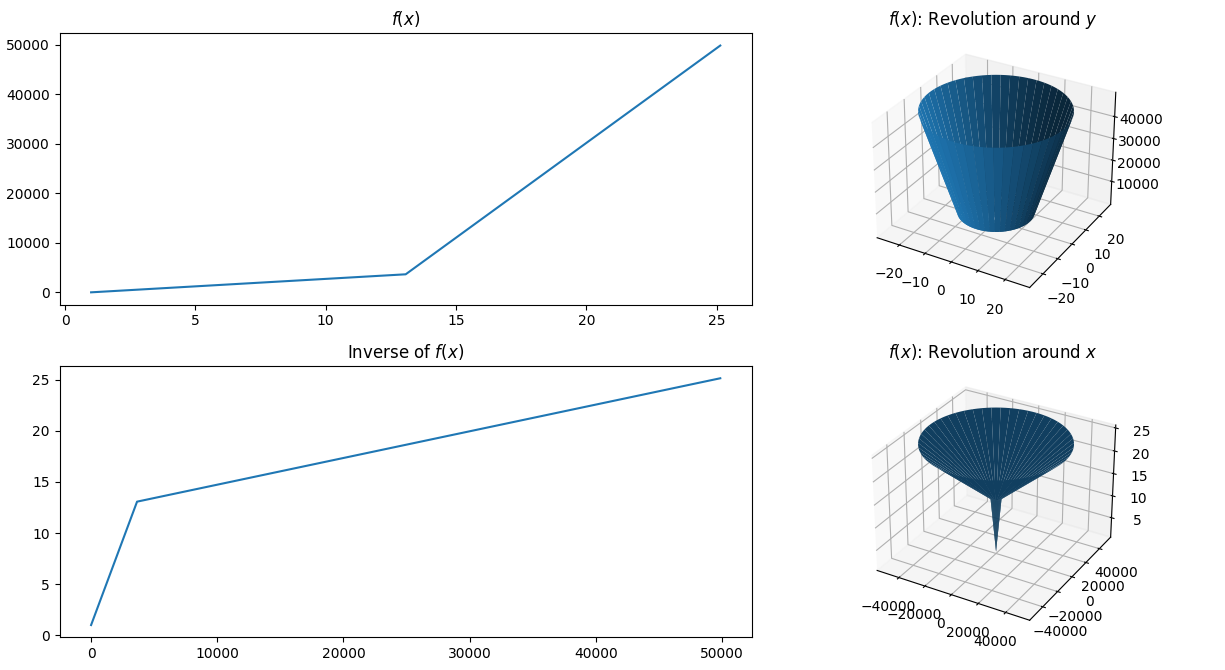
I want to plot area of surface of

(x^6 2)/(8x^2)

with 1 ≤ x ≤ 3

this is my Python code / MWE:

import matplotlib.pyplot as plt
import numpy as np

n = 100

fig = plt.figure(figsize=(14, 7))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222, projection='3d')
ax3 = fig.add_subplot(223)
ax4 = fig.add_subplot(224, projection='3d')
x = np.linspace(1, 3, 3)
y = ((x ** 6)   2) / (8 * x ** 2)
t = np.linspace(0, np.pi * 2, n)

xn = np.outer(x, np.cos(t))
yn = np.outer(x, np.sin(t))
zn = np.zeros_like(xn)
for i in range(len(x)):
    zn[i:i   1, :] = np.full_like(zn[0, :], y[i])

ax1.plot(x, y)
ax1.set_title("$f(x)$")
ax2.plot_surface(xn, yn, zn)
ax2.set_title("$f(x)$: Revolution around $y$")

# find the inverse of the function
y_inverse = x
x_inverse = ((y_inverse ** 6)   2) / ( 8 * x ** 2)
xn_inverse = np.outer(x_inverse, np.cos(t))
yn_inverse = np.outer(x_inverse, np.sin(t))
zn_inverse = np.zeros_like(xn_inverse)
for i in range(len(x_inverse)):
    zn_inverse[i:i   1, :] = np.full_like(zn_inverse[0, :], y_inverse[i])

ax3.plot(x_inverse, y_inverse)
ax3.set_title("Inverse of $f(x)$")
ax4.plot_surface(xn_inverse, yn_inverse, zn_inverse)
ax4.set_title("$f(x)$: Revolution around $x$")

plt.tight_layout()
plt.show()

Questions:

1. I want to know whether the plot is correct for the surface area.
2. Is there any better way to plot besides this ?
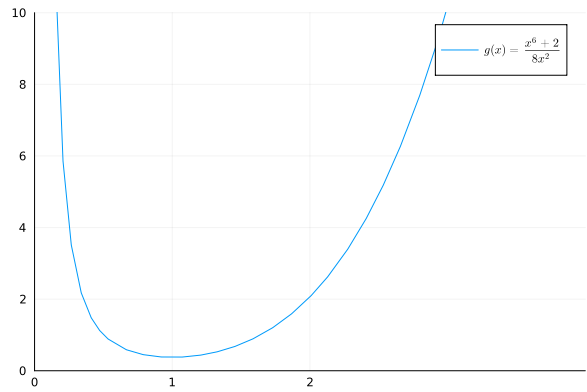
3. I think the plot of y, the x-axis and y-axis limit need more adjustment, since I use Julia to plot the function and got this (more smooth curve not bending):

CodePudding user response：

when you do

x = np.linspace(1, np.pi * 40 / 5, 3)

the variable x will contain a numpy array from 1 to np.pi * 40 / 5 with only 3 values, if you want to smooth the function you will need to change the 3 for a bigger number like 100 or 1000, this value will be the size of x.