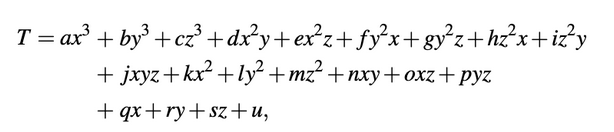I'm trying to solve the following formula via least squares:
Data:
dat <- structure(list(x = c(-3.06315207481384, -3.53966951370239, -0.786132514476776,
2.85316586494446, 1.91431069374084, 0.238738358020782, -2.71875023841858,
-4.51564025878906, -1.76425766944885, 36.0447616577148, 36.2231864929199,
35.088565826416, 14.5400581359863, 11.0608978271484, 13.5029678344727,
9.24409198760986, 9.52021884918213, 11.5315561294556, 9.64649677276611,
-7.40514183044434, -5.99363708496094, -8.3693323135376, -6.55220413208008,
16.6599369049072, 15.3896722793579, 14.0078706741333, -5.96392107009888,
-6.05945920944214, -3.35051441192627, -4.49518489837646), y = c(-100.958953857422,
-96.9687881469727, -99.6262283325195, -59.8251037597656, -61.4415702819824,
-63.2435073852539, -99.5627517700195, -104.385040283203, -102.582824707031,
-62.4078750610352, -60.3811149597168, -63.3329849243164, -87.6252822875977,
-86.7032775878906, -89.111930847168, -48.4490776062012, -44.3725166320801,
-44.0625152587891, -49.8619041442871, -99.2568817138672, -101.303993225098,
-101.118591308594, -104.259971618652, -59.4827270507812, -61.4948043823242,
-59.0172729492188, -114.305473327637, -113.537368774414, -115.28190612793,
-115.021911621094), z = c(213.060043334961, 214.551696777344,
214.275970458984, 186.614593505859, 189.293151855469, 185.896148681641,
190.264511108398, 192.610168457031, 190.945388793945, 196.600631713867,
197.723648071289, 197.753433227539, 179.977508544922, 180.026229858398,
181.597991943359, 193.011459350586, 193.536712646484, 195.603088378906,
194.673904418945, 212.374145507812, 212.009017944336, 210.889434814453,
210.546630859375, 212.190979003906, 212.855712890625, 211.486724853516,
203.421585083008, 205.626281738281, 206.354309082031, 202.603637695312
), activation_timing_ms = c(-8.95099963430584, -11.000197429963,
-8.00000000000023, -29.3800032106763, -25.0499782952136, -29.9494419934181,
-6.33357028643786, -7.84766776411197, -7, 4.41525051236772, 11,
6.54840968699932, 8.55739954149135, -15.6434811032107, 15, -6.4484910424228,
-7.04479069209742, -12.0007923079093, -8.9730733157603, -8.37403162067676,
-9.07784949298457, -10.8114914004932, -6.9208993234206, -33.6635361890419,
-27.2229083353382, -33.3012393050494, 1.82628266289839, 2, 0,
1)), row.names = c(NA, 30L), class = "data.frame")
So I wrote:
lm <- lm(activation_timing_ms ~ x^3 y^3 z^3
x^2*y x^2*z y^2*x y^2*z z^2*x z^2*y x*y*z
x^2 y^2 z^2 x*y x*z y*z x y z,
data = dat)
Which doesn't do what I expected since it's only returning the linear components and the interactions.
coef(lm)
(Intercept) x y z x:y
-3.930285e 02 6.376611e 01 -4.131947e 00 1.754539e 00 5.855662e-01
x:z y:z x:y:z
-3.100900e-01 1.895621e-02 -2.830448e-03
Thanks for the help!
CodePudding user response:
You need to use I() function inside lm
From the help file you can read:
In function formula. There it is used to inhibit the interpretation of operators such as " ", "-", "*" and "^" as formula operators, so they are used as arithmetical operators. This is interpreted as a symbol by terms.formula.
lm(activation_timing_ms ~ I(x^3) I(y^3) I(z^3)
I(x^2)*y I(x^2)*z I(y^2)*x I(y^2)*z I(z^2)*x I(z^2)*y x*y*z
I(x^2) I(y^2) I(z^2) x*y x*z y*z x y z,
data = dat)
Coefficients:
(Intercept) I(x^3) I(y^3) I(z^3) I(x^2) y z I(y^2) x
-5.514e 04 -1.263e-02 5.575e-04 5.903e-03 2.991e 00 -2.699e 01 8.109e 02 6.264e-01 -2.756e 02
I(z^2) I(x^2):y I(x^2):z I(y^2):x z:I(y^2) x:I(z^2) y:I(z^2) y:x z:x
-3.847e 00 1.291e-02 -8.344e-03 -6.022e-03 -2.320e-03 -2.948e-03 -3.120e-03 -2.483e 00 1.737e 00
y:z y:z:x
8.326e-01 6.996e-03
CodePudding user response:
You could use
lm(activation_timing_ms~polym(x,y,z, degree=3, raw = TRUE), dat)
or even
lm(activation_timing_ms~poly(cbind(x,y,z), 3, raw = TRUE), dat)
which results in:
summary(my_model)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.514e 04 4.439e 04 -1.242 0.2425
poly(cbind(x, y, z), 3, raw = TRUE)1.0.0 -2.756e 02 3.265e 02 -0.844 0.4183
poly(cbind(x, y, z), 3, raw = TRUE)2.0.0 2.991e 00 2.364e 00 1.266 0.2344
poly(cbind(x, y, z), 3, raw = TRUE)3.0.0 -1.263e-02 1.430e-02 -0.883 0.3980
poly(cbind(x, y, z), 3, raw = TRUE)0.1.0 -2.699e 01 2.217e 02 -0.122 0.9055
poly(cbind(x, y, z), 3, raw = TRUE)1.1.0 -2.483e 00 1.246e 00 -1.993 0.0742 .
poly(cbind(x, y, z), 3, raw = TRUE)2.1.0 1.291e-02 1.639e-02 0.788 0.4492
poly(cbind(x, y, z), 3, raw = TRUE)0.2.0 6.264e-01 4.625e-01 1.354 0.2055
poly(cbind(x, y, z), 3, raw = TRUE)1.2.0 -6.022e-03 7.728e-03 -0.779 0.4539
poly(cbind(x, y, z), 3, raw = TRUE)0.3.0 5.575e-04 1.575e-03 0.354 0.7307
poly(cbind(x, y, z), 3, raw = TRUE)0.0.1 8.109e 02 6.611e 02 1.227 0.2481
poly(cbind(x, y, z), 3, raw = TRUE)1.0.1 1.737e 00 2.891e 00 0.601 0.5614
poly(cbind(x, y, z), 3, raw = TRUE)2.0.1 -8.344e-03 5.993e-03 -1.392 0.1940
poly(cbind(x, y, z), 3, raw = TRUE)0.1.1 8.326e-01 2.294e 00 0.363 0.7241
poly(cbind(x, y, z), 3, raw = TRUE)1.1.1 6.996e-03 8.067e-03 0.867 0.4061
poly(cbind(x, y, z), 3, raw = TRUE)0.2.1 -2.320e-03 3.316e-03 -0.699 0.5002
poly(cbind(x, y, z), 3, raw = TRUE)0.0.2 -3.847e 00 3.381e 00 -1.138 0.2818
poly(cbind(x, y, z), 3, raw = TRUE)1.0.2 -2.948e-03 7.442e-03 -0.396 0.7003
poly(cbind(x, y, z), 3, raw = TRUE)0.1.2 -3.120e-03 6.741e-03 -0.463 0.6534
poly(cbind(x, y, z), 3, raw = TRUE)0.0.3 5.903e-03 5.973e-03 0.988 0.3463