create a circle, divide it into circular sectors and test where a point is located with R-CodePudding

I need your help to create a code that allows me to project points in a circular grid, divided into segments and levels. I'm asking for your help, because I know that this community is full of great people.

What I would like to do is

create a circle in a Cartesian plane; the coordinates of its centre point must be x=300 and y=300 and its radius r=300;
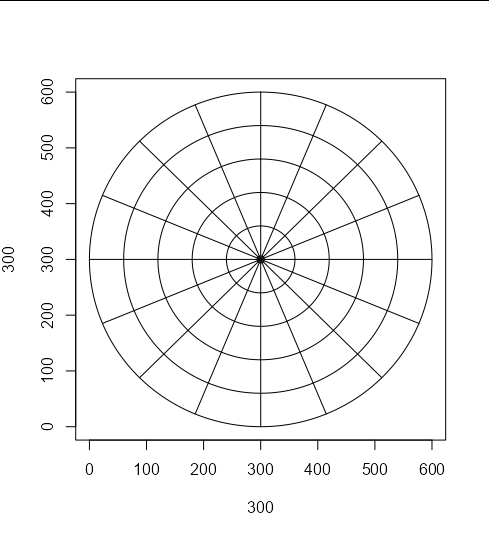
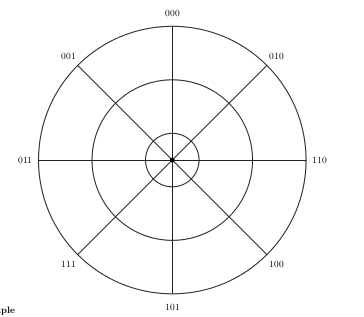
after constructing the circle, I need to divide it into portions. I need to construct a grid similar to the one you see below, but with 16 segments (with 16 labels, e.g. sector_1 to sector_16) and 5 levels or concentric circles (with 5 labels, e.g. level_1 to level_4 level_0 for the central circle). So I would need to construct 5 concentric circles and divide the second, third, fourth and fifth into 16 segments. My aim is to obtain a series of regions in which a point could fall;

Circular Grid

after constructing this grid, I need to project in it some points that I have and of which I have the x and y coordinates (e.g. point_1 -> x=286; y=342);

R should return to me in which segment and at which level the point is located.

Please, how can I develop code that allows me to do this?

Any help is so welcome and helpful.

Thank you very much for your attention.

CodePudding user response：

You can draw the grid like this:

t <- seq(0, 2 * pi, length = 1000)

plot(300, 300, xlim = c(0, 600), ylim = c(0, 600))

for(i in 0:4) {
  lines((300 - (i * 60)) * sin(t)   300, (300 - (i * 60)) * cos(t)   300)
}

for(i in 0:7) {
  lines(300 * sin(c(i * pi /8, i * pi / 8   pi))   300,
        300 * cos(c(i * pi /8, i * pi / 8   pi))   300)
}

To calculate in which segment the point has landed, you calculate the distance from the centre of the circle and find the whole number of 60s this exceeds

sqrt((x - 300)^2   (y - 300)^2) %/% 60

To find out which segment it belongs in, you need to find its polar angle, which you can get by:

atan2((y - 300), (x - 300))

And you can determine which segment this represents by finding the number of pi/8 it exceeds:

atan2((y - 300), (x - 300)) %/% pi/8