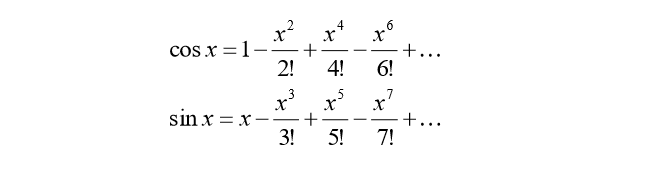Hi I am trying to calculate the results of the Taylor series expansion for sine to the specified number of terms.

I am running into some problems

• Your task is to implement makeSineToOrder(k)
• This is templated by the type of values used in the calculation.
• It must yield a function that takes a value of the specified type and
• returns the sine of that value (in the specified type again)

double factorial(double long order){

#include <iostream> 
#include <iomanip> 
#include <cmath> 

double fact = 1;

for(int i = 1; i <= num; i  ){

    fact *= i;

}

return fact;
}

  

  

  void makeSineToOrder(long double order,long double precision = 15){
double value = 0;

for(int n = 0; n < precision; n  ){

    value  = pow(-1.0, n) * pow(num, 2*n 1) / factorial(2*n   1);

}

return value; 
int main()

    {
         using namespace std;
        long double pi = 3.14159265358979323846264338327950288419716939937510L;
        for(int     order = 1;order < 20; order  ) {
              auto sine = makeSineToOrder<long double>(order);
               cout << "order(" << order << ") -> sine(pi) = " << setprecision(15) << sine(pi) << endl;
          }
          return 0;
       }

I tried debugging

CodePudding user response：

here is a version that at least compiles and gives some output

#include <iostream> 
#include <iomanip> 
#include <cmath> 
using namespace std;
double factorial(double long num) {
    double fact = 1;
    for (int i = 1; i <= num; i  ) {
        fact *= i;
    }
    return fact;
}

double makeSineToOrder(double num, double precision = 15) {
    double value = 0;

    for (int n = 0; n < precision; n  ) {

        value  = pow(-1.0, n) * pow(num, 2 * n   1) / factorial(2 * n   1);

    }
    return value;
}

int main(){

    long double pi = 3.14159265358979323846264338327950288419716939937510L;
    for (int order = 1; order < 20; order  ) {
        auto sine = makeSineToOrder(order);
        cout << "order(" << order << ") -> sine(pi) = " << setprecision(15) << sine << endl;
    }
    return 0;
}

not sure what that odd sine(pi) was supposed to be doing

CodePudding user response：

Apart the obvious syntax errors (the includes should be before your factorial header) in your code:

1. I see no templates in your code which your assignment clearly states to use

   so I would expect template like:

   <class T> T mysin(T x,int n=15){ ... }
   

2. using pow for generic datatype is not safe

   because inbuild pow will use float or double instead of your generic type so you might expect rounding/casting problems or even unresolved function in case of incompatible type.

   To remedy that you can rewrite the code to not use pow as its just consequent multiplication in loop so why computing pow again and again?

3. using factorial function is waste

   you can compute it similar to pow in the same loop no need to compute the already computed multiplications again and again. Also not using template for your factorial makes the same problems as using pow

so putting all together using this formula:

along with templates and exchanging pow,factorial functions with consequent iteration I got this:

template <class T> T mysin(T x,int n=15)
    {
    int i;
    T y=0;      // result
    T x2=x*x;   // x^2
    T xi=x;     // x^i
    T ii=1;     // i!
    if (n>0) for(i=1;;)
        {
        y =xi/ii; xi*=x2; i  ; ii*=i; i  ; ii*=i; n--; if (!n) break;
        y-=xi/ii; xi*=x2; i  ; ii*=i; i  ; ii*=i; n--; if (!n) break;
        }
    return y;
    }

so factorial ii is multiplied by i 1 and i 2 every iteration and power xi is multiplied by x^2 every iteration ... the sign change is hard coded so for loop does 2 iterations per one run (that is the reason for the break;)

As you can see this does not use anything funny so you do not need any includes for this not even math ...

You might want to add x=fmod(x,6.283185307179586476925286766559) at the start of mysin in order to use more than just first period however in that case you have to ensure fmod implementation uses T or compatible type to it ... Also the 2*pi constant should be in target precision or higher

beware too big n will overflow both int and generic type T (so you might want to limit n based on used type somehow or just use it wisely).

Also note on 32bit floats you can not get better than 5 decimal places no matter what n is with this kind of computation.

Btw. there are faster and more accurate methods of computing goniometrics like Chebyshev and CORDIC