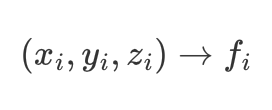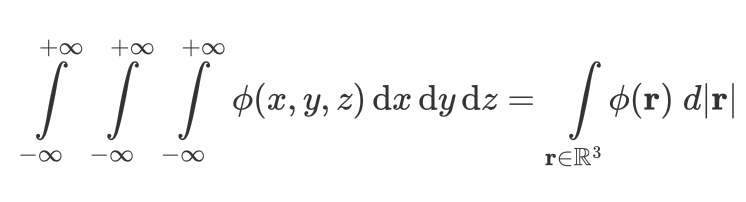3D integral in Python from a discrete set of points?-CodePudding

I am looking to calculate an integral in 3D with a function with pre-defined values on an irregular grid.

In particular, my grid coords and the values at these points combined is of the shape

<        coords = self._grid.coords - pos
<        print(coords.shape)

>        (2328, 3)

**

<       combined = self._q * self._grid.weights / d
<       print(combined.shape)

>      (2328,)

I don't really know how to proceed to get the integral of combined assuming the three components of coords run from negative ifinity to positive infinity. I looked up the built in packages of numpy and scipy (for example scipy.integrate.quad) but my understanding is that you need to have a function that's defined at every point in space to use those options. Is there any nice approach to numerically integrate when the function is only given at a discrete non-uniform grid?

CodePudding user response：

You have a scalar discrete function of form

And want to integrate

Here, ϕ is a "continious" version of f. To integrate this, you have several options.

Look for integration using samples, this kind of integration is for discrete-defined functions (e.g. f). But, it looks like scipy does not have a version for triple integal. Start to google packages by "python trapezoidal/simpson rule 3d".
You may interpolate discrete function f and get approximation of ϕ (interpolant). So, you need this scipy.interpolate, and then put the interpolant to scipy.integration.tplquad. (Actually, this is how quadrature rules are analytically derived.)

To treat infinity limits, iteratively expand the limits (just some large number relative to your grid edges) and observe, how the integral value changes to decide, which precision is OK for you. In that case, the value of integral should approach some limit. Or... plot the function and decide where to truncate it.

Also, there is another family of integrators based on Monte Carlo method.

For brief introduction to numerical integration, see FNC: Numerical integration.

CodePudding user response：

You could try Gaussian quadrature if you already have a grid established. Use a master Lagrangian local element, a local-to-global Jacobean mapping, the grid geometry, and the function to do the numerical integration.

This is common in finite element analysis. Look at FEA texts to see the details.