I have a data.table test_dt, in which some of the values are missing for each group. Can someone suggest the fastest way to interpolate and fill the missing value?
In the graph form x-axis is column a and y-axis is column b, hench the interval distance of column a should be considered while predicting b.
test_dt = structure(list(group = c("B1", "B1", "B1", "B1", "B1", "B1", "B1", "B1", "C1", "C1", "C1", "C1", "C1", "C1", "C1", "C1"), a = c(165, 170, 185, 195, 200, 210, 220, 240, 1, 1.5, 2, 4.5, 5, 5.5, 7, 10), b = c(1.925, 0.575, 0.3, NA, NA, 2.825, 9.05, 27.9, 3.775, 3.225, 2.75, 0.255, 0.04, NA, NA, NA)), row.names = c(NA, -16L), class = c("data.table", "data.frame"), index = integer(0))
> test_dt
group a b
1: B1 165.0 1.925
2: B1 170.0 0.575
3: B1 185.0 0.300
4: B1 195.0 NA
5: B1 200.0 NA
6: B1 210.0 2.825
7: B1 220.0 9.050
8: B1 240.0 27.900
9: C1 1.0 3.775
10: C1 1.5 3.225
11: C1 2.0 2.750
12: C1 4.5 0.255
13: C1 5.0 0.040
14: C1 5.5 NA
15: C1 7.0 NA
16: C1 10.0 NA
Following are some conditions -
- Interpolated values should not be zero or negative value
- Interpolated values should not be a copy of the last non-NA value
I tried to solve it using na.spline but the result is not correct, especially for group C1, where value of column a is 7 and 10
test_dt[, predicted := zoo::na.spline(zoo(.SD), x = a)[, 2], by = c("group")]
> test_dt
group a b predicted
1: B1 165.0 1.925 1.92500000
2: B1 170.0 0.575 0.57500000
3: B1 185.0 0.300 0.30000000
4: B1 195.0 NA 0.18981191
5: B1 200.0 NA 0.40167712
6: B1 210.0 2.825 2.82500000
7: B1 220.0 9.050 9.05000000
8: B1 240.0 27.900 27.90000000
9: C1 1.0 3.775 3.77500000
10: C1 1.5 3.225 3.22500000
11: C1 2.0 2.750 2.75000000
12: C1 4.5 0.255 0.25500000
13: C1 5.0 0.040 0.04000000
14: C1 5.5 NA 0.03038963
15: C1 7.0 NA 1.67389631
16: C1 10.0 NA 16.44642968
Update - 1 Following is the second dataset. Using the solutions below, the predicted values are very high.
temp_dt = structure(list(group = c("K1", "K1", "K1", "K1", "K1", "K1",
"K1", "K1", "K1", "K1", "K1", "K1", "K1", "F1", "F1", "F1", "F1",
"F1", "F1"), a = c(185, 190, 195, 200, 202.5, 205, 210, 212.5,
215, 217.5, 220, 222.5, 225, 22, 23, 24, 25, 26, 35), b = c(NA,
NA, 0.45, 0.6, 1.05, 1.45, 2.7, 3.125, 4.3, NA, 7.05, 8.95, 10.35,
0.5, 0.7, 0.925, 1.2, 1.75, NA), predicted = c(463741.812236,
14.7721571, 0.45, 0.6, 1.05, 1.45, 2.7, 3.125, 4.3, 5.6346081,
7.05, 8.95, 10.35, 0.5, 0.7, 0.925, 1.2, 1.75, 65226323253857.9
)), row.names = c(NA, -19L), class = c("data.table", "data.frame"
), .internal.selfref = <pointer: 0x563cccc504c0>, index = integer(0))
test_dt[, predicted := round(exp(na.spline(log(b), x = a, na.rm = FALSE)), 7), by = group]
group a b predicted
1: K1 185.0 NA 4.637418e 05
2: K1 190.0 NA 1.477216e 01
3: K1 195.0 0.450 4.500000e-01
4: K1 200.0 0.600 6.000000e-01
5: K1 202.5 1.050 1.050000e 00
6: K1 205.0 1.450 1.450000e 00
7: K1 210.0 2.700 2.700000e 00
8: K1 212.5 3.125 3.125000e 00
9: K1 215.0 4.300 4.300000e 00
10: K1 217.5 NA 5.634608e 00
11: K1 220.0 7.050 7.050000e 00
12: K1 222.5 8.950 8.950000e 00
13: K1 225.0 10.350 1.035000e 01
14: F1 22.0 0.500 5.000000e-01
15: F1 23.0 0.700 7.000000e-01
16: F1 24.0 0.925 9.250000e-01
17: F1 25.0 1.200 1.200000e 00
18: F1 26.0 1.750 1.750000e 00
19: F1 35.0 NA 6.522632e 13
CodePudding user response:
There are infinite ways to do this, each way having a certain set of assumptions. Here is one way, transforming the data into the log scale, performing linear interpolation, and then exponentiating the result. This should approach 0 but not be exactly 0.
library(zoo)
round(exp(na.spline(log(test_dt$b),na.rm=F,method="natural")),5)
[1] 1.92500 0.57500 0.30000 0.39398 0.96937 2.82500 9.05000 27.90000 3.77500
[10] 3.22500 2.75000 0.25500 0.04000 0.00835 0.00175 0.00036
Also you should perform this separately for each group, so that there is no interpolation between groups.
CodePudding user response:
Ultimately, you have to decide the interpolation procedure based on scientific background. However, in order to avoid producing negative values, the log-transformation is useful. In the following, I combine that with a spline interpolation.
library(data.table)
test_dt = data.table(group = c("B1", "B1", "B1", "B1", "B1", "B1",
"B1", "B1", "C1", "C1", "C1", "C1", "C1", "C1", "C1", "C1"),
a = c(165, 170, 185, 195, 200, 210, 220, 240, 1, 1.5, 2, 4.5, 5, 5.5, 7, 10),
b = c(1.925, 0.575, 0.3, NA, NA, 2.825, 9.05, 27.9, 3.775, 3.225, 2.75, 0.255,
0.04, NA, NA, NA))
library(zoo)
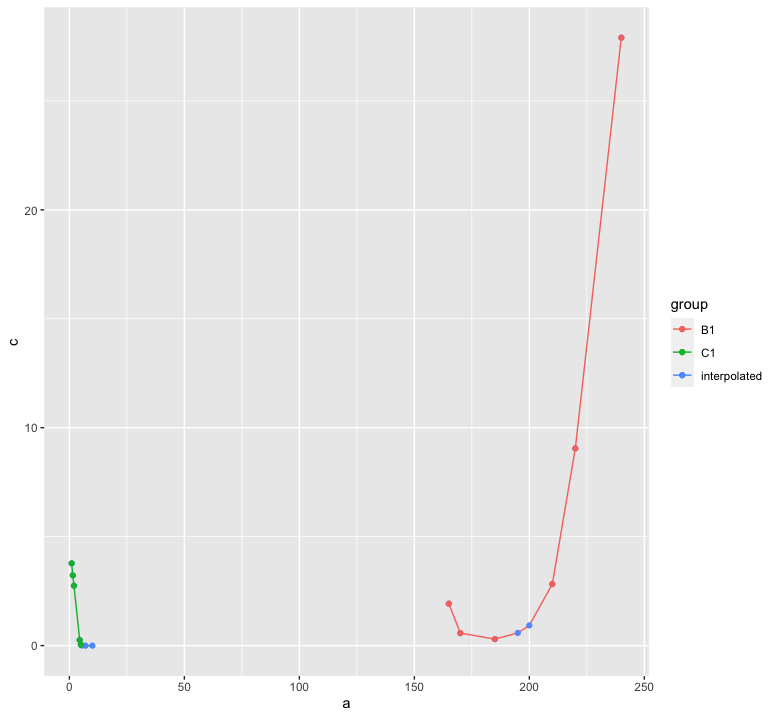
test_dt[, c := exp(na.spline(log(b), x = a, na.rm = FALSE)), by = group]
library(ggplot2)
ggplot(test_dt, aes(x = a, color = group))
geom_line(aes(y = c))
geom_point(aes(y = c, color = "interpolated"))
geom_point(aes(y = b))
CodePudding user response:
Try different methods of spline.
Also here I catch values lower than 0.0001 with pmax.
met <- c("fmm", "natural", "monoH.FC")
cbind(test_dt, lapply(setNames(met, met), function(met) {
ave(seq_len(nrow(test_dt)), test_dt$group, FUN=function(i) {
pmax(0.0001, splinefun(test_dt$a[i], test_dt$b[i], met)(test_dt$a[i]))
}) }) )
# group a b fmm natural monoH.FC
#1 B1 165.0 1.925 1.92500000 1.9250000 1.9250000
#2 B1 170.0 0.575 0.57500000 0.5750000 0.5750000
#3 B1 185.0 0.300 0.30000000 0.3000000 0.3000000
#4 B1 195.0 NA 0.18981191 0.2372716 0.3751691
#5 B1 200.0 NA 0.40167712 0.4448177 0.6702794
#6 B1 210.0 2.825 2.82500000 2.8250000 2.8250000
#7 B1 220.0 9.050 9.05000000 9.0500000 9.0500000
#8 B1 240.0 27.900 27.90000000 27.9000000 27.9000000
#9 C1 1.0 3.775 3.77500000 3.7750000 3.7750000
#10 C1 1.5 3.225 3.22500000 3.2250000 3.2250000
#11 C1 2.0 2.750 2.75000000 2.7500000 2.7500000
#12 C1 4.5 0.255 0.25500000 0.2550000 0.2550000
#13 C1 5.0 0.040 0.04000000 0.0400000 0.0400000
#14 C1 5.5 NA 0.03038963 0.0001000 0.0001000
#15 C1 7.0 NA 1.67389631 0.0001000 0.0001000
#16 C1 10.0 NA 16.44642968 0.0001000 0.0001000