Handling very precise numbers in R-CodePudding

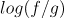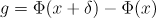I am using R to try and solve the formula where and 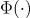is the standard normal distribution function. The problem I run into is that some values of g are very small or coded in R as 0 so that the given solution is Inf. An example of when g is coded as 0 when it should be positive is given in the line of code below.

pnorm(29.1,0,1) - pnorm(29,0,1) #this returns a value of 0

In light of this problem I have two questions. First, is there a mathematical trick which can be used to get a positive number from the above code? I know there is a pnorm argument log.p=TRUE which returns the log of the probability. Perhaps that could come in handy?

My second question is, in the case where I have a positive but very small g, is there a mathematical trick for ensuring the log of the ratio of f and g is finite?

CodePudding user response：

As pointed out in answers and comments, you really only need to compute log(g).

One solution is to use logspace addition/subtraction, which uses a nice trick to compute log(exp(x) ± exp(y)) accurately.

DPQ::logspace.sub(pnorm(29.1, log.p = TRUE), pnorm(29, log.p = TRUE))
## [1] -424.8435

@Alex points out that if we look at the (symmetric) opposite tail by reversing the signs, so that we are subtracting a very small number from another very small number, the round-off error isn't a problem:

log(pnorm(-29,0,1) - pnorm(-29.1,0,1))
##  -424.8435

Comparing the derivative-based estimate from @GregorThomas:

dnorm(29, log = TRUE)   log(0.1)
## [1] -423.7215

Checking these solutions with the Rmpfr package:

library(Rmpfr)
x1 <- mpfr(29.1, 1000)  ### 1000-bit precision
x2 <- mpfr(29.0, 1000)
log(pnorm(x1) - pnorm(x2))
## 1 'mpfr' number of precision  1000   bits 
## [1] -424.843525917118620331088762368642820931865149932737039093516330881321230653835360169156688142607902967369067320263733953321675429119215305576014352760866238194504221709021981332048618426550583180796866417925580695487036011142823944123174363138216647098415472494704193913895461975221571930136768807682871

So it looks like @GregorThomas's solution is pretty close, but the other two solutions are better.

CodePudding user response：

log(f / g) = log(f) - log(g), so you need to calculate log(g).

You have g = pnorm(x d) - pnorm(x).

The density function (dnorm() in R)is the derivative of the CDF (pnorm()). This means that dnorm(x) = (pnorm(x delta) - pnorm(x)) / delta as delta approaches 0. So for small delta we can approximate dnorm(x) * delta = pnorm(x delta) - pnorm(x). Thus g(x) = dnorm(x) * d (approximately), and log(g(x)) = log(dnorm(x)) log(d).

Use dnorm(29, log = TRUE) log(0.1) in your calculation as log(g).