In the following code I wanted to generate a color heatmap (w x h x 3) based on the values of a NumPy 2-d array, in the range [-1; 1], and, unsurprisingly, it is really slow on large arrays (10000 x 10000) compared to the rest of the program, which uses NumPy numerical operations. Colors are in the [B, G, R] format.
def img_to_heatmap(arr):
height, width = arr.shape
heatmap = np.zeros((height, width, 3))
for i in range(width):
for j in range(height):
val = arr[i,j]
if(val < 0): # [-1 to 0)
val = 1
heatmap[i,j,:] = [0, val * 255, 255] # red -> yellow
else: # [0 to 1]
heatmap[i,j,:] = [0, 255, 255 - 255*val] # yellow -> green
return heatmap
How can this code run faster while using the exact same color map? I know OpenCV has built-in heatmap calculations, but not the exact color map I want.
CodePudding user response:
you could use np.where to find the index and vectorize your loops:
def img_to_heatmap1(arr):
height, width = arr.shape
heatmap = np.zeros((height * width, 3))
heatmap[:, 1:] = 255
arr = arr.reshape(-1)
idx = np.where(arr < 0)
nidx = np.where(arr >= 0)
heatmap[idx, 1] = 255 * (arr[idx] 1)
heatmap[nidx, 2] -= 255 * arr[nidx]
return heatmap.reshape((height , width, 3))
for an image of 1K x 1K this will be roughly 20X speedup.
CodePudding user response:
As per your comment under your question -
For example, -1 will display full bright red, -0.5 orange, 0 yellow, 0.5 lime, 1 green
IIUC, you are trying to display a large matrix as a heatmap where you can set the color maps at fixed static values but, the color mixing should happen automatically. For example - if you have set 0 as yellow, 1 as green, then 0.5 should have a lemon-green color.
Approach 1: Numpy first then plot
If you are interested in only the matrix manipulated, then you can do this simply by using numpy -
import numpy as np
import matplotlib.pyplot as plt
def heatmap_raw(arr):
scale = np.interp(arr, (-1, 1), (0, 1)) #convert -1 to 1 -> 0 to 1
R = np.where((1-scale)>=0.5,255,255*(1-scale)) #red layer
G = np.where(scale<0.5,255*scale,255) #green layer
B = np.zeros_like(arr) #blue layer
#stack, transpose and round
raw = np.round(np.stack([R, G, B])).transpose(1,2,0).astype(np.uint8)
return raw
arr = np.array([[-1, -0.5, 0, 0.5, 1]])
print(heatmap_raw(arr))
plt.imshow(heatmap_raw(arr))
# RGB values (H,W,3) array shape
array([[[255., 0., 0.], #<- -1 is red
[255., 64., 0.], #<- -0.5 is orange
[255., 255., 0.], #<- 0 is yellow
[ 64., 255., 0.], #<- 0.5 is lemon green
[ 0., 255., 0.]]]) #<- 1 is green
Benchmark for a (10000,10000) array -
%%timeit
arr = np.random.uniform(low=-1, high=1, size=(10000,10000))
heatmap_raw(arr)
14.5 s ± 924 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Approach 2: Plotting only using custom cmap
If your goal ultimately is to visualize, you can directly jump to creating a custom CMAP in matplotlib and then plot the heatmap using seaborn. Note, this takes a bit of time to render but that is expected.
import numpy as np
from matplotlib import colors
import matplotlib.pyplot as plt
import seaborn as sns
def heatmap_custom(arr):
cvals = [-1, 0, 1] #<- only define colors for..
clrs = ["red","yellow","green"] #<- ..the key checkpoints
norm = plt.Normalize(min(cvals),max(cvals))
tuples = list(zip(map(norm,cvals), clrs))
cmap = colors.LinearSegmentedColormap.from_list("", tuples)
sns.heatmap(arr, cmap=cmap)
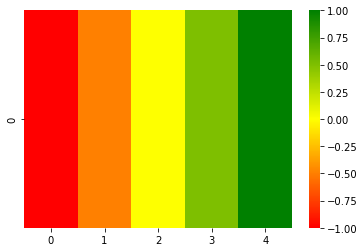
arr = np.array([[-1, -0.5, 0, 0.5, 1]]) #<- dummy array with the example you mentioned
heatmap_custom(arr)
For example, -1 will display full bright red, -0.5 orange, 0 yellow, 0.5 lime, 1 green
Another example -
arr = np.random.uniform(low=-1, high=1, size=(50,50))
heatmap_custom(arr)
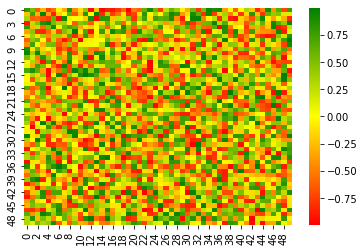
Example with (10000, 10000) shaped matrix -
arr = np.random.uniform(low=-1, high=1, size=(10000,10000))
heatmap_custom(arr)
Bonus (additional experimentation)
I was playing around with some transformations that can better help distinguish colors when building a heatmap. Here is the updated code and experimental results for anyone who is interested!
import numpy as np
import matplotlib.pyplot as plt
#Transformations to better distinguish color gradient
sinfx = lambda x: np.sin(2*x)
cubefx = lambda x: np.power(x, 3)
expfx = lambda x: np.exp(x)
customfx = lambda x: 1-np.exp(-1*x)
def heatmap_raw(arr, transform = False, fx=None):
"""
Input: np.array(m,n), 2D matrix with values
Output: np.array(m,n,3) with values ranging from 0 to 255
Additional Parameters:
- transform (Optional) -> Bool
- fx (Optional) -> transformation function
Create a heatmap matrix (RGB) shaped (m,n,3) as an image tensor.
1. Applies any transformation (Optional)
2. Normalizes distribution to 0 to 1 scale for multiplications
3. Applies R, G, B conditions based on custom logic
4. Stacks, Round, Transposes the output before returning
"""
#Normalize (after applying transformation (optional))
if transform == True:
transformed = fx(arr)
scale = np.interp(transformed, (transformed.min(), transformed.max()), (0, 1))
else:
scale = np.interp(arr, (arr.min(), arr.max()), (0, 1))
#Create custom R, G, B based on rules
R = np.where((1-scale)>=0.5,255,255*(1-scale)) #red layer
G = np.where(scale<0.5,255*scale,255) #green layer
B = np.zeros_like(arr) #blue layer
#Stack, Round and Transpose
raw = np.round(np.stack([R, G, B])).transpose(1,2,0).astype(np.uint8)
return raw
Experiment without a transformation -
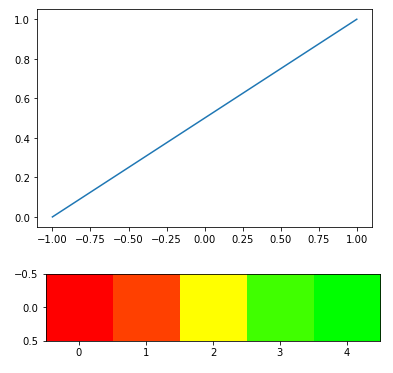
# Plotting transformations with their relation to original
arr = np.array([[-1, -0.5, 0, 0.5, 1]])
scale = np.interp(arr, (-1, 1), (0, 1))
plt.plot(arr[0], scale[0])
plt.show()
#Heatmap scale
output = heatmap_raw(arr)
plt.imshow(output)
plt.show()
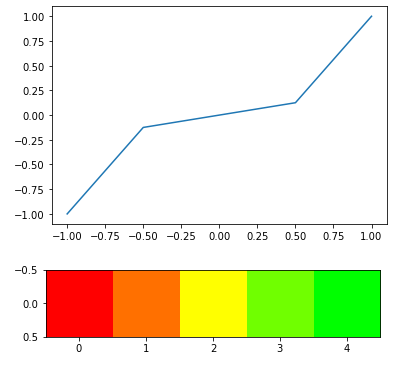
Experiment with sin(2*x) -
# Plotting transformations with their relation to original
arr = np.array([[-1, -0.5, 0, 0.5, 1]])
scale = sinfx(arr)
plt.plot(arr[0], scale[0])
plt.show()
#Heatmap scale
output = heatmap_raw(arr, transform=True, fx=sinfx)
plt.imshow(output)
plt.show()
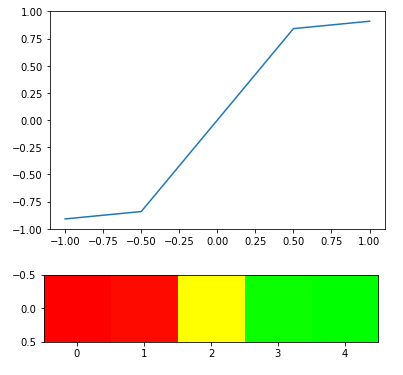
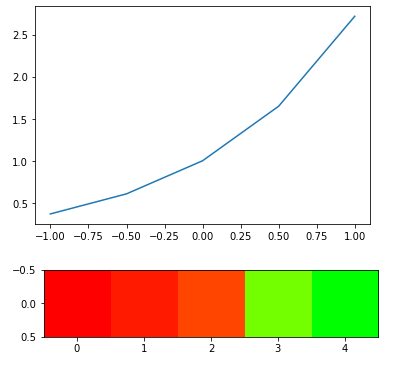
Experiment with cube(x) -
# Plotting transformations with their relation to original
arr = np.array([[-1, -0.5, 0, 0.5, 1]])
scale = cubefx(arr)
plt.plot(arr[0], scale[0])
plt.show()
#Heatmap scale
output = heatmap_raw(arr, transform=True, fx=cubefx)
plt.imshow(output)
plt.show()
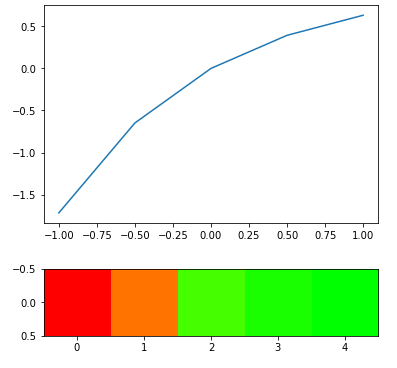
Experiment with exp(x) -
# Plotting transformations with their relation to original
arr = np.array([[-1, -0.5, 0, 0.5, 1]])
scale = expfx(arr)
plt.plot(arr[0], scale[0])
plt.show()
#Heatmap scale
output = heatmap_raw(arr, transform=True, fx=expfx)
plt.imshow(output)
plt.show()
Experiment with 1-exp(-x) -
# Plotting transformations with their relation to original
arr = np.array([[-1, -0.5, 0, 0.5, 1]])
scale = customfx(arr)
plt.plot(arr[0], scale[0])
plt.show()
#Heatmap scale
output = heatmap_raw(arr, transform=True, fx=customfx)
plt.imshow(output)
plt.show()
The cube(x) really helps distinguish the extreme values due to the nature of its distribution.